CS50 Week 5 Data Structure¶
基本的数据结构。
数组 Array 的弊端¶
数组中的元素是连续储存在内存中的,也就是说:相邻的元素在内存中是“紧挨”着的。
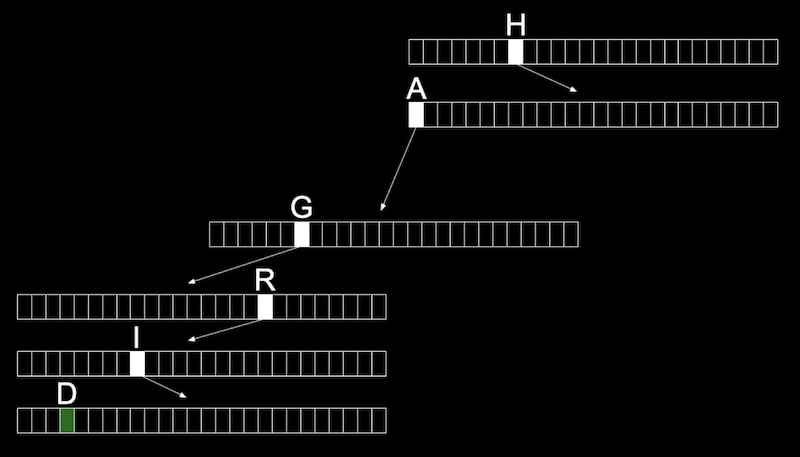
当我们已经有一个数组[1, 2, 3],它的后面(紧挨的右边的内存)已经被其它量(在下图中,是字符串h)占用了。

如果我们需要向这个数组中添加一个元素4,可行的办法是:重新分配一块大小为 4 的内存,先把原数组[1, 2, 3]复制到新内存上,再添上4。
这样的做法很耗费时间,因为我们每次遇到内存冲突的情况时(形象地说,就是想要写入的元素碰到 Corner 了,没办法在相邻的内存继续写入元素了),都需要完整地把原数组复制一遍。如果原数组很大,那么复制过程会很漫长。
链表¶
思想¶
为每一个元素额外再分配一个内存,这个新内存用来储存“下一个元素的地址”。这样,即便每个元素的地址不需要是相邻的,计算机也能知道各个元素的先后顺序。
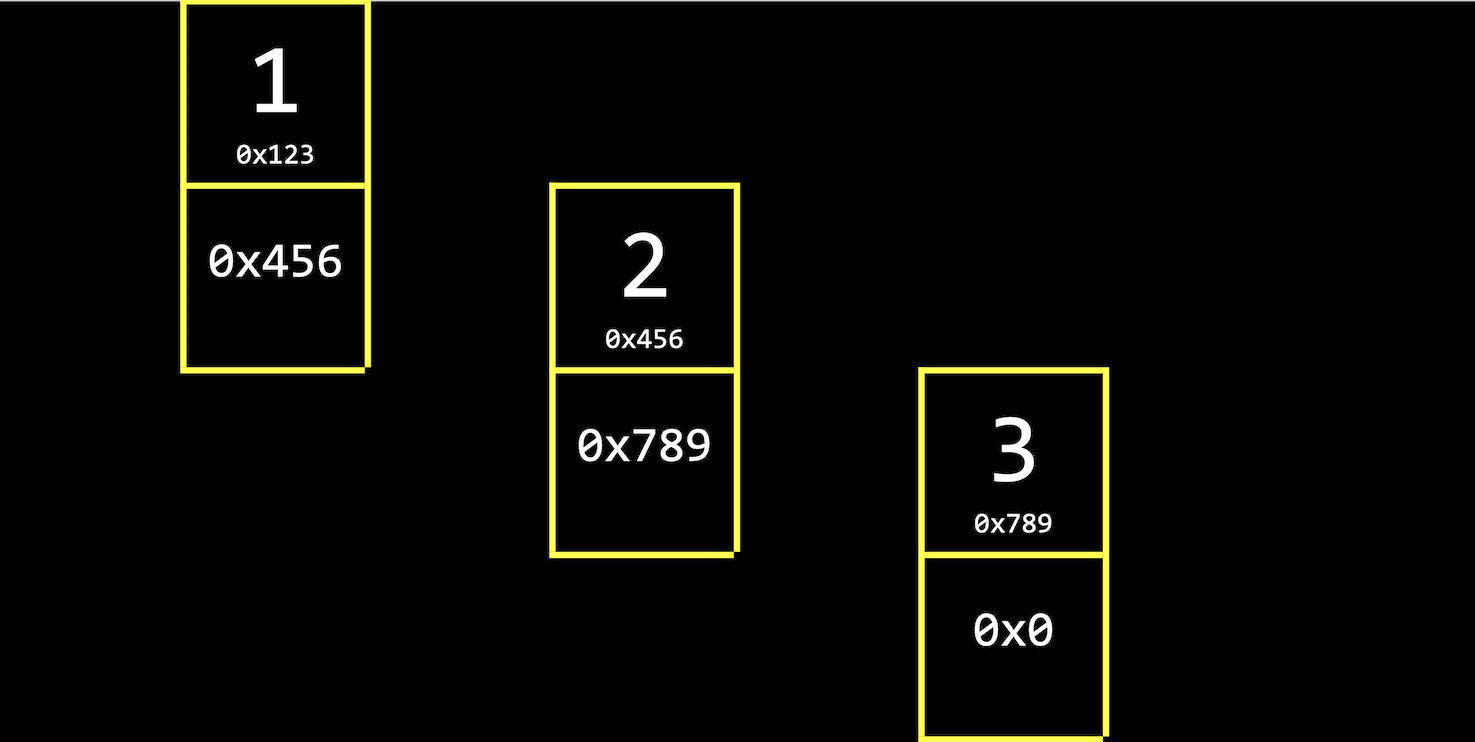
对于最后一个元素来说,它额外储存的是0x0,即空地址,代表没有下一个元素了。
空间和时间的权衡¶
- 链表需要额外储存下一个元素的地址,而数组不需要。因此链表需要更多的内存空间。
- 链表在插入新元素时避免了“相邻地址被占用”的问题,因此不需要复制原数组。因此链表节约了时间。
定义链表的数据结构¶
初始化链表¶
新建一个变量,初始化为空值。若不初始化为空值,可能会得到垃圾值。
在链表上添加节点¶
//分配内存
node *n = malloc(sizeof(node));
//检查是否还有内存剩余
if (n != NULL)
{
//给节点赋值
n->number = 1;
n->next = NULL;
}
树¶
每个节点不仅储存自身的数字,还储存:
- 左节点,它比当前节点小;
- 右节点,它比当前节点大。
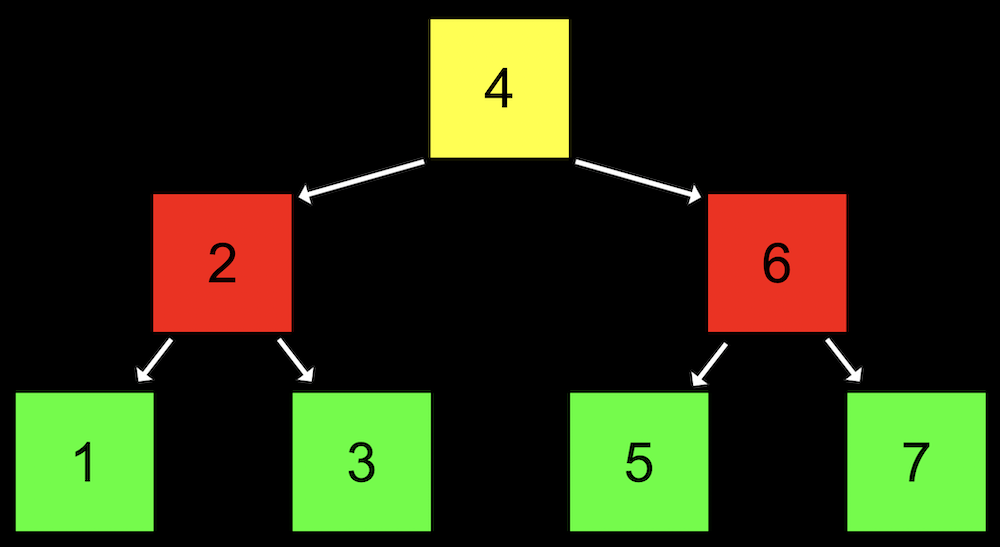
定义树形结构:¶
初始化一个树根:¶
int main(void)
{
// Tree of size 0
node *tree = NULL;
// Add number to list
node *n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 2;
n->left = NULL;
n->right = NULL;
tree = n;
添加子节点¶
在左边添加节点:
// Add number to list
n = malloc(sizeof(node));
if (n == NULL)
{
free_tree(tree);
return 1;
}
n->number = 1;
n->left = NULL;
n->right = NULL;
tree->left = n;
在右边添加节点:
// Add number to list
n = malloc(sizeof(node));
if (n == NULL)
{
free_tree(tree);
return 1;
}
n->number = 3;
n->left = NULL;
n->right = NULL;
tree->right = n;
// Print tree
print_tree(tree);
// Free tree
free_tree(tree);
return 0;
上面的代码用到了print_tree函数,它是一个典型的递归写法:
void print_tree(node *root)
{
if (root == NULL)
{
return;
}
print_tree(root->left);
printf("%i\n", root->number);
print_tree(root->right);
}
free_tree函数的代码,它同样也是递归的写法:
void free_tree(node *root)
{
if (root == NULL)
{
return;
}
free_tree(root->left);
free_tree(root->right);
free(root);
}
树的搜索(递归算法)¶
bool search(node *tree, int number)
{
if (tree == NULL)
{
return false;
}
else if (number < tree->number)
{
return search(tree->left, number);
}
else if (number > tree->number)
{
return search(tree->right, number);
}
else if (number == tree->number)
{
return true;
}
}
低效率的树¶
一个平衡的树结构的搜索复杂度应该是\(O(\log n)\)。
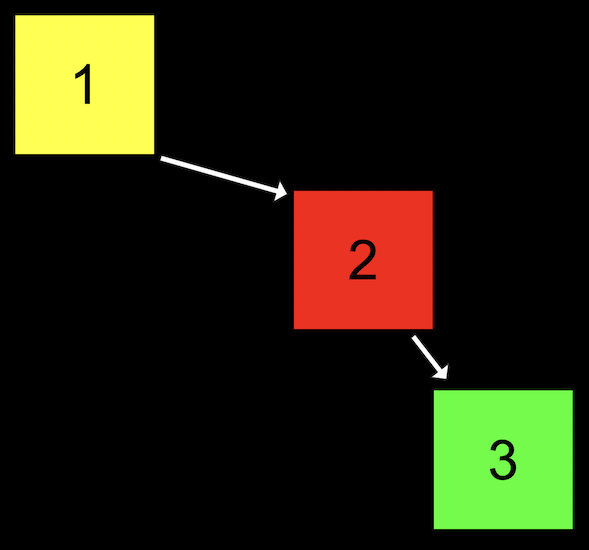
下面的树结构并没有用到左节点,而仅仅是在右边添加节点,它和链表没有什么区别,因此搜索效率是\(O(n)\)。
哈希表¶
将所有的名字按照首字母分类,就是哈希表的思想:
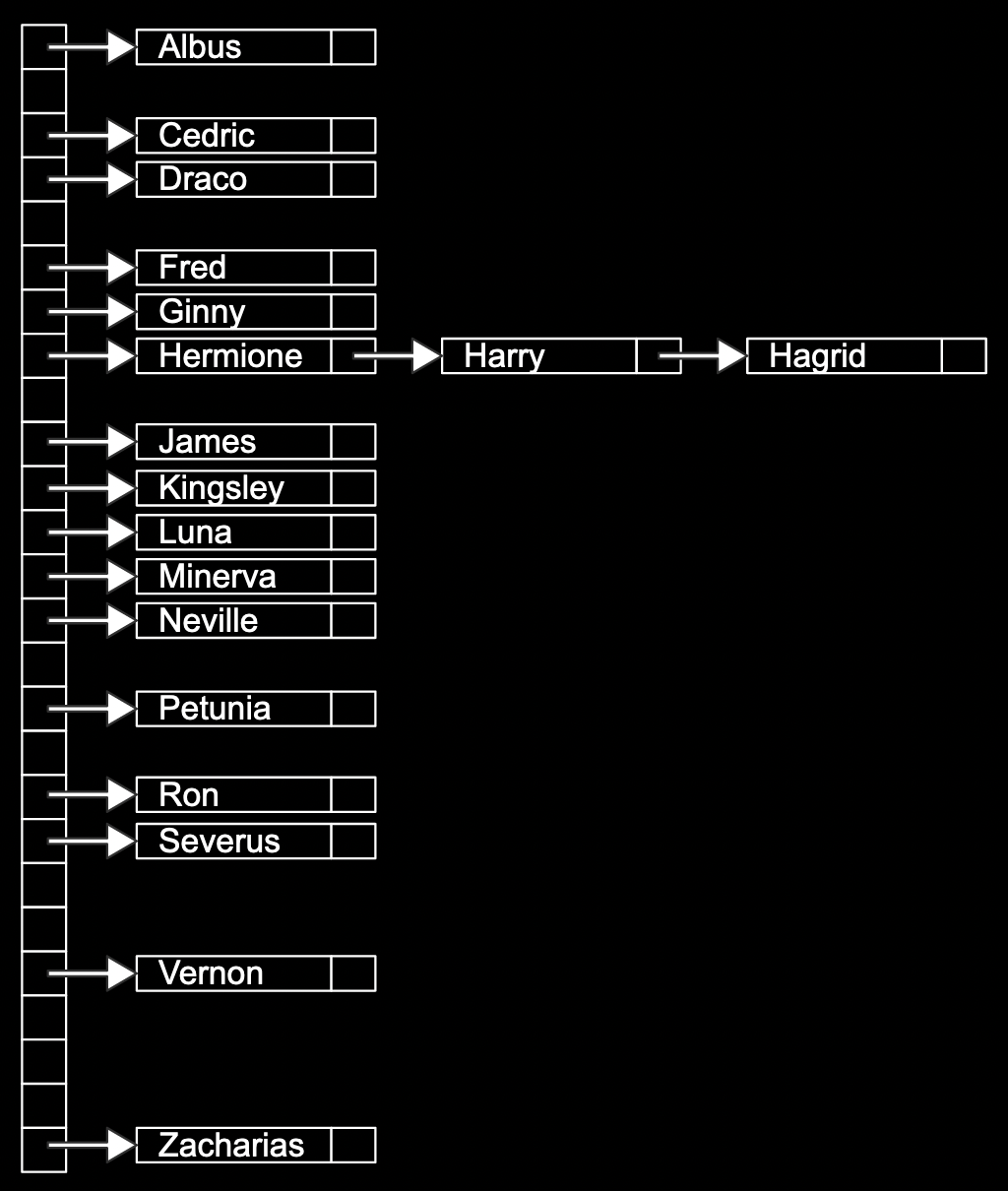
使用这种哈希表,比常规的链表快 26 倍。
Trie 结构¶
这种结构的搜索复杂度是 Constant 的。即使储存了 1 万个、10 万个名字,搜索每一个名字的时间仍然是这个名字的字符串长度。
但 Trie 结构并不经常被使用,因为它需要非常多的内存。如图所示,名字的第一个字母需要 26 个字符,每一个字符后面又跟着 26 个字符,即第二个字母需要 26*26 个字符,第三个字母需要 26*26*26 个字符,最后需要非常多的字符来储存。
队列¶
先进先出。像在商店排队,最先进去的人最先离开。
栈¶
后进先出。像一个一个堆起来的餐盘,最上面的餐盘是最后被放上去的,但它确却是最先被拿出的。