AlphaNet

思路框架

问题背景

传统的因子挖掘过程通常是由人工构造因子表达式，对多个单因子进行加权合成。面对大量的原始数据，人工基于投资经验，手动构造因子表达式生成单因子的过程是极其繁琐的。在因子合成阶段，通常是用ICIR加权平均等手段进行合成，这种简单的线性加权方式也限制了因子合成的多种可能性。

将卷积思想应用于因子挖掘

在卷积神经网络中，最关键的特征提取组件是卷积核。在图像识别领域，卷积核通过一个带有可优化的权重和偏置项的矩阵，对原始数据进行互相关操作。

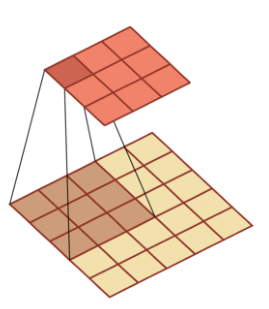
我们可以将原始量价数据整理成一个二维矩阵，尝试使用卷积核对数据进行特征提取。

但是，如果完全采用传统的卷积操作，提取的特征就是：一定感受野范围内的特征的加权组合。这样的操作会有两个问题：

提取的特征只是某些特征数据的固定的加权组合，这极大地限制了因子表达式的可能性。
传统的卷积核只能感受局部范围内的数据，因此，我们输入的特征变量的上下顺序会影响提取出的特征。因此输入变量的顺序还需要人工干预。

由此看来，简单地套用卷积操作并不合适，但我们可以借鉴卷积核的“遍历操作”的思想，自定义运算符函数，实现类似“卷积层”的特征提取层。

具体的特征提取层将在后文介绍。经过特征提取后，可再添加批标准化层、池化层、全连接层，将原始数据转换为收益率的预测。

优化模型

对于上述将卷积思想应用于因子挖掘的方法，可以尝试对两个方向进行优化。

调整网络结构。添加更丰富的特征提取层，将池化层转换为可以记忆时序信息的循环神经网络。
调整标签值。将收益率值得预测转换为涨跌方向的预测和超额收益率方向的预测。

准备数据集

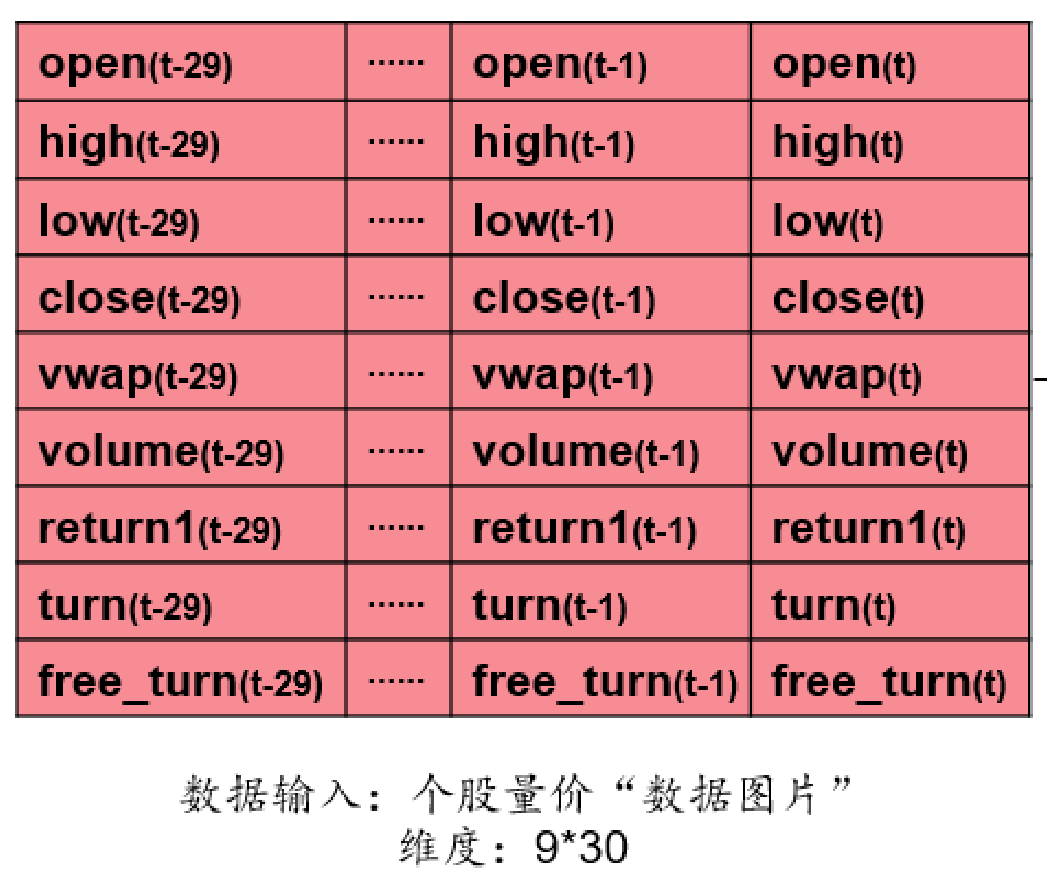
我们需要的特征均为量价数据，即open, high, low, close, vwap, volume, return1, turn, free_turn这9个量价指标在$t-29$到$t$时间段的$9\times 30$个特征。

Tushare提供了免费的量价数据接口，在程序中导入token，即可使用pro.daily()下载数据。

下面具体介绍获取数据的细节。

训练集和测试集包含的时间段

由于通过Tushare的免费接口获取数据的速度较慢（逐股票、逐日获取后再合并，而不是批量一次性获取，因此耗时较久），本文只截取了20220101至20220630这半年的数据作为训练集，20220930至20221231这一季度的数据作为测试集。没有用20220630至20221231的数据作为测试集，是因为希望训练集和验证集之间能够暂停一段时间，否则训练集的标签可能会包含未来信息，进而夸大测试集上的预测效果。

本项目下载数据的时间为2022年12月初，因此实际所用的验证集并不是完整的一季度。

采样的日期

如果对训练集和验证集包含的时间段中的每一个交易日均进行采样，会造成两个问题：

采样过于频繁，导致相邻日期的数据基本相近。
采样天数过多，下载数据的时间会非常久。

因此，本文使用间隔采样的方法，每间隔10个交易日进行一次采样。具体判断哪一天为采样日的函数为：

# 给定日期区间的端点，输出期间的定长采样交易日列表
def get_datelist(start: str, end: str, interval: int):

    df = pro.index_daily(ts_code='399300.SZ', start_date=start, end_date=end)
    date_list = list(df.iloc[::-1]['trade_date'])
    sample_list = []
    for i in range(len(date_list)):
        if i % interval == 0:
            sample_list.append(date_list[i])

    return sample_list

其原理是基于沪深300指数（399300.SZ）的交易数据进行间隔采样。沪深300指数有数据的日期一定是交易日。

采样的股票

A股市场的股票数量近5000只，若对每一只股票均进行采样也将耗费大量时间。本文对每个采样日，获取前1000只股票的数据。具体判断对哪些股票进行采样的函数为：

# 给定一个交易日，返回该日满足条件的A股股票列表
def get_stocklist(date: str, num: int):

    start = str(pd.to_datetime(date)-timedelta(30))
    start = start[0:4]+start[5:7]+start[8:10]
    df1 = pro.index_weight(index_code='000002.SH',
                           start_date=start, end_date=date)  # 交易日当天的股票列表
    codes = list(df1['con_code'])
    codes = codes[0:1000]  # 在每个截面期只选取1000只股票

    return codes

其原理是基于A股指数（000002.SH）的前1000只成分股进行采样。

获取单个股票在单个交易日的数据

get_x_y()函数返回两个值，一个是前30个交易日的9个指标面板（9*30），一个是未来10天的收益率。

def get_x_y(code: str, date: str, pass_day: int, future_day: int, len1: int, len2: int):

    start = str(pd.to_datetime(date)-timedelta(pass_day*2))
    start = start[0:4]+start[5:7]+start[8:10]
    end = str(pd.to_datetime(date)+timedelta(future_day*2))
    end = end[0:4]+end[5:7]+end[8:10]
    df_price = pro.daily(ts_code=code,  # OHLC,pct_change,volume
                         start_date=start, end_date=date)
    df_basic = pro.daily_basic(ts_code=code,
                               start_date=start, end_date=date)
    df_return = pro.daily(ts_code=code,
                          start_date=date, end_date=end).iloc[::-1]['close']
    if (df_price.shape[0] == df_basic.shape[0]) & (df_price.shape[0] == len1) & (df_return.shape[0] == len2):  # 判断数据的完整性
        df_price = df_price.iloc[0:pass_day, [2, 3, 4, 5, 8, 9]].fillna(0.1)
        df_basic = df_basic.iloc[0:pass_day, [3, 4, 5]].fillna(0.1)
        data = np.array(pd.merge(df_price, df_basic,
                        left_index=True, right_index=True).iloc[::-1].T)
        # print(data.shape)
        # 未来十个交易日的收益率
        dfr = df_return.iloc[0:future_day]
        ret = dfr.iloc[-1]/dfr.iloc[0]-1  # 后十个交易日的收益率
        return data, ret
    else:
        return None, None  # 数据缺失的预处理

舍弃缺失值

在获取单个股票在单个交易日的数据时，若某只股票的数据有缺失，则需舍弃它，否则在输入到神经网络时会带有缺失值。

基于沪深300指数，判断某日应有的数据长度的函数：

def get_length(date: str, pass_day: int, future_day: int):
    start = str(pd.to_datetime(date)-timedelta(pass_day*2))
    start = start[0:4]+start[5:7]+start[8:10]
    end = str(pd.to_datetime(date)+timedelta(future_day*2))
    end = end[0:4]+end[5:7]+end[8:10]
    len_1 = pro.index_daily(ts_code='399300.SZ',
                            start_date=start, end_date=date).shape[0]
    len_2 = pro.index_daily(ts_code='399300.SZ',
                            start_date=date, end_date=end).shape[0]
    return len_1, len_2

在get_x_y()函数中，基于len_1和len_2判断了数据的完整性。若有缺失值则返回空值，不会计入数据集中。

获取数据集

筛选出哪一天、哪一只股票需要进行采样后，我们就可以获取数据了。

对每一个采样日、每一只股票进行循环。配合rich.progress可以展示下载数据的进度条。

rich.progress的使用示例可以参考这里。

def get_dataset(num: int, start: str, end: str, interval: int, pass_day: int, future_day: int):
    X_train = []
    y_train = []
    trade_date_list = get_datelist(start, end, interval)
    # 添加进度条
    with Progress() as progress:
        task_date = progress.add_task(
            "[red]Date...", total=len(trade_date_list))
        for date in trade_date_list:
            # 更新进度条
            progress.update(task_date, advance=1)
            stock_list = get_stocklist(date, num)
            len1, len2 = get_length(date, pass_day, future_day)
            task_stock = progress.add_task(
                "[green]Stock...", total=len(range(len(stock_list))))
            for i in range(len(stock_list)):
                # 更新进度条
                progress.update(task_stock, advance=1)
                code = stock_list[i]
                x, y = get_x_y(code, date, pass_day, future_day, len1, len2)
                try:
                    if (x.shape[0] == 9) & (x.shape[1] == pass_day):
                        X_train.append(x)
                        y_train.append(y)
                except Exception:
                    continue
    return X_train, y_train

数据示例：

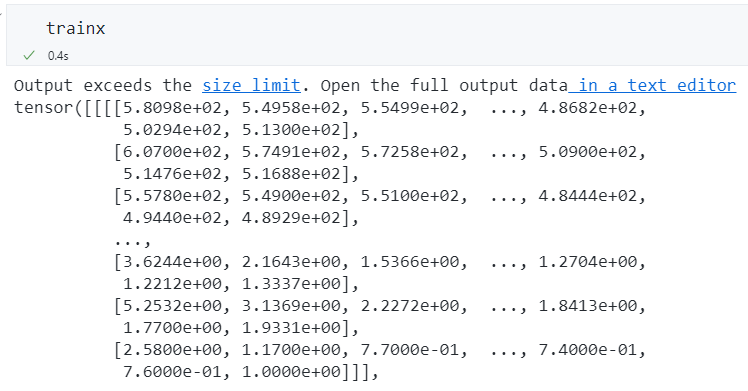
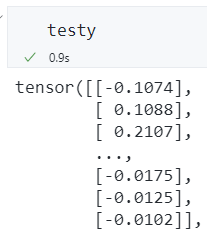
保存`.npy`数据到本地

为了方便训练模型，可以将数据以.npy格式存储到本地。在训练模型时可以直接使用np.load('../data/X_train.npy')载入数据。

# 参数设定：使用过去30天的数据预测未来10天的收益率，回归问题
X_train, y_train = get_dataset(
    num=1000, start='20220101', end='20220630', interval=10, pass_day=30, future_day=10)
X_test, y_test = get_dataset(num=1000, start='20220931',
                             end='20221231', interval=10, pass_day=30, future_day=10)
print("there are in total", len(X_train), "training samples")
print("there are in total", len(X_test), "testing samples")
# 将数据保存到本地供离线训练
Xa = np.array(X_train)
ya = np.array(y_train)
Xe = np.array(X_test)
ye = np.array(y_test)
np.save('./X_train.npy', Xa)
np.save('./y_train.npy', ya)
np.save('./X_test.npy', Xe)
np.save('./y_test.npy', ye)

整个获取数据的时间约为3个小时，共获取到11825条训练数据和4943条测试数据（数据量不为1000的整数倍，是因为舍弃了部分缺失值）。

特征数据为$9\times 30$的个股量价数据构成的矩阵。9行代表9个量价特征，30代表$t-29$至$t$这30天的数据。
标签数据为个股在某个交易日往后10个交易日的收益率。

搭建AlphaNet-V1

AlphaNet-V1的整体网络结构

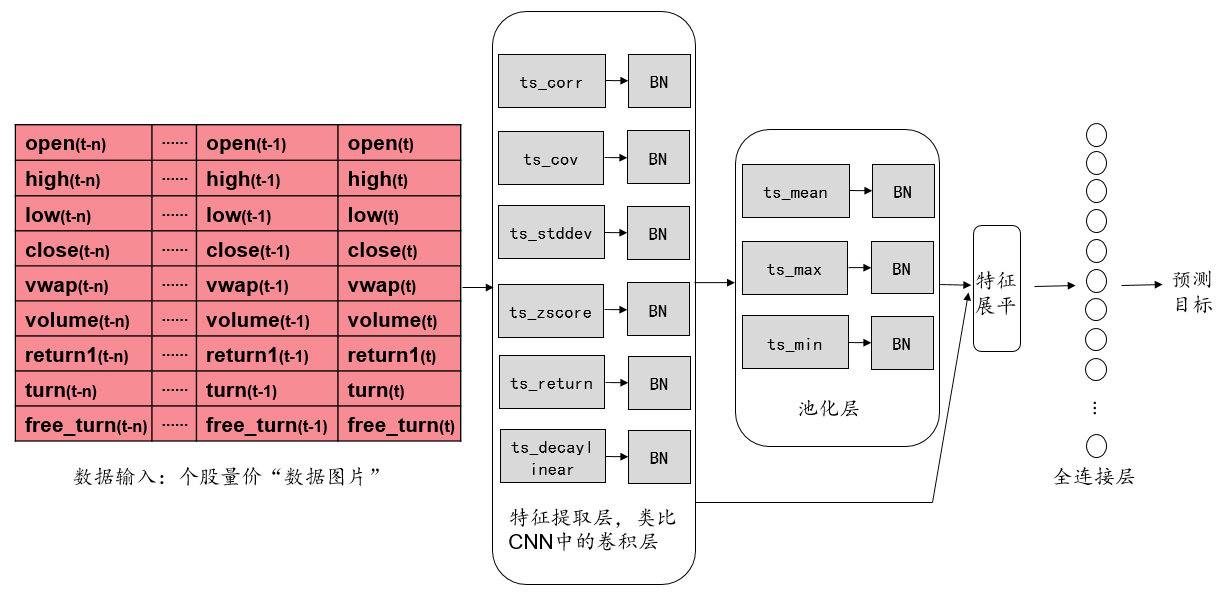
下图展示了AlphaNet-V1的整体网络结构。它由7个平行的特征提取层、3个平行的池化层和1个全连接层组成。其中，特征提取层和池化层后都有一个批标准化层（Batch Normalization）。

输入数据是一个$9\times30$的个股量价“数据图片”，预测目标为个股从当日到10个交易日后的收益率数值。

特征提取层（类似卷积层）

AlphaNet的输入数据是一个$9\times30$的个股量价“数据图片”。如果简单地套用卷积神经网络处理图片像素数据的操作，则卷积操作只能在感受野内将若干日期的若干量价数据进行加权平均，经过卷积层得到的特征将变得很难解释，也不符合传统构造量价因子的方式。

因此，借鉴卷积神经网络CNN的思想，我们可以将多种运算符函数作为自定义网络层进行特征提取。本文实现了7种运算符，分别是ts_corr, ts_cov, ts_stddev, ts_zscore, ts_return, ts_decaylinear, ts_mean，它们的含义如下：

名称	定义
`ts_corr`	过去 d 天 X 值构成的时序数列和 Y 值构成的时序数列的相关系数。
`ts_cov`	过去 d 天 X 值构成的时序数列和 Y 值构成的时序数列的协方差。
`ts_stddev`	过去 d 天 X 值构成的时序数列的标准差。
`ts_zscore`	过去 d 天 X 值构成的时序数列的平均值除以标准差。
`ts_return`	(X - delay(X, d))/delay(X, d)-1, delay(X, d)为 X 在 d 天前的取值。
`ts_decaylinear`	过去 d 天 X 值构成的时序数列的加权平均值，权数为 d, d – 1, …, 1(权数之和应为 1，需进行归一化处理)，其中离现在越近的日子权数越大。
`ts_mean`	过去 d 天 X 值构成的时序数列的平均值。

这7个运算符函数中，ts_corr和ts_cov需要从9行数据中提取2行数据，并计算相关系数和协方差。其他5个运算符函数仅需针对某一行数据计算标准差、变化率等。下面针对这两种情况分别举例说明。

基于双变量的特征提取层——以`ts_corr`为例

我们的输入数据是$9\times30$的矩阵，每一行是某个量价指标在最近30个交易日的值。基于双变量进行特征提取的步骤为：

取出两行数据。
对于取出的两行数据，给定步长stride，在时间维度上对两行数据进行遍历，计算两行数据的相关系数。例如，当$stride=3$时，下一次计算将在时间维度上往右步进3步，我们将进行$\frac{30}{3}=10$次运算。
将运算结果整理到新的矩阵，得到新的“特征图片”，作为后续池化层的输入。

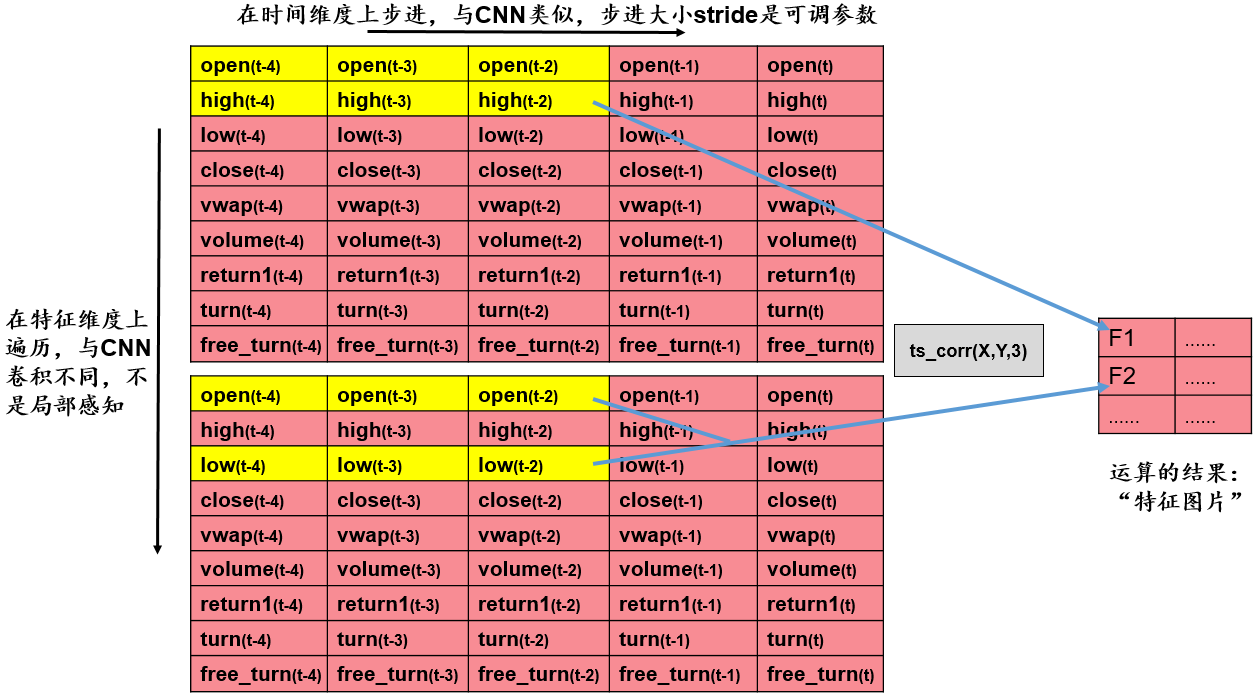
从9行数据中任取2行，有$\tbinom{9}{2}=36$种取法。假设我们设定步长为10，则得到的新的“特征图片”的维数是$36\times3$。

基于双变量的特征提取层——代码实现

需要给定原始矩阵Matrix、两两组合的列表combination、反转的两两组合的列表combination_rev以及每次遍历运算的起始索引列表index_list。

生成combination和combination_rev的代码为：

# 生成卷积操作时需要的两列数据的组合的列表
def generate_combination(N):
    """
    args:
        N: int, the number of rows of the matrix

    return:
        combination: list, the combination of two columns of the matrix
        combination_rev: list, the combination of two rows of the matrix, which is the reverse of combination
    """
    col = []
    col_rev = []
    for i in range(1,N):
        for j in range(0,i):
            col.append([i,j])
            col_rev.append([j,i])
    return col, col_rev
# 生成卷积操作时需要的两列数据的组合的列表
combination, combination_rev = generate_combination(9)

生成index_list的代码为：

# 根据输入的矩阵和卷积操作的步长, 计算卷积操作的索引
def get_index_list(matrix, stride):
    """
    args:
        matrix: torch.tensor, the input matrix
        stride: int, the stride of the convolution operation
    
    return:
        index_list: list, the index of the convolution operation

    """
    W = matrix.shape[3]
    if W % stride == 0:
        index_list = list(np.arange(0, W+stride, stride))
    else:
        mod = W % stride
        index_list = list(np.arange(0, W+stride-mod, stride)) + [W]
    return index_list
# 根据输入的矩阵和卷积操作的步长, 计算卷积操作的索引
# Inception模块使用的卷积操作的步长为10
index_list = get_index_list(np.zeros((1,1,9,30)), 10)

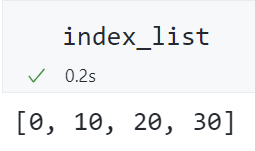
基于双变量的特征提取代码为：

# 过去 d 天 X 值构成的时序数列和 Y 值构成的时序数列的相关系数
def ts_corr4d(self, Matrix, combination, combination_rev):
    new_H = len(combination)
    index_list = self.index_list
    list = []  # 存放长度为len(index_list)-1的相关系数
    for i in range(len(index_list)-1):
        start_index = index_list[i]
        end_index = index_list[i+1]
        data = Matrix[:, :, combination, start_index:end_index]  # N*1*new_H*2*d
        data2 = Matrix[:, :, combination_rev,
                        start_index:end_index]  # N*1*new_H*2*d
        std1 = data.std(axis=4, keepdims=True)  # N*1*new_H*2*1, 在时序上求标准差
        std2 = data2.std(axis=4, keepdims=True)  # N*1*new_H*2*1, 在时序上求标准差
        std = (std1*std2).mean(axis=3, keepdims=True)  # N*1*new_H*1*1
        list.append(std)
    std = np.squeeze(np.array(list)).transpose(1, 2, 0).reshape(-1, 1, new_H, len(index_list)-1)+0.01  # N*1*new_H*len(index_list)-1 # 加上0.01, 防止除0
    # N*1*new_H*len(index_list)-1
    cov = self.ts_cov4d(Matrix, combination, combination_rev)
    corr = cov/std  # N*1*new_H*len(index_list)-1
    return corr

# 过去 d 天 X 值构成的时序数列和 Y 值构成的时序数列的协方差
def ts_cov4d(self, Matrix, combination, combination_rev):
    new_H = len(combination)
    index_list = self.index_list
    list = []  # 存放长度为len(index_list)-1的协方差
    for i in range(len(index_list)-1):
        start_index = index_list[i]
        end_index = index_list[i+1]
        data = Matrix[:, :, combination, start_index:end_index]  # N*1*new_H*2*d
        data2 = Matrix[:, :, combination_rev,
                        start_index:end_index]  # N*1*new_H*2*d
        mean1 = data.mean(axis=4, keepdims=True)  # N*1*new_H*2*1, 在时序上求均值
        mean2 = data2.mean(axis=4, keepdims=True)  # N*1*new_H*2*1, 在时序上求均值
        spread1 = data - mean1  # N*1*new_H*2*d, 在时序上求偏差
        spread2 = data2 - mean2  # N*1*new_H*2*d, 在时序上求偏差
        cov = ((spread1 * spread2).sum(axis=4, keepdims=True) /
                (data.shape[4]-1)).mean(axis=3, keepdims=True)  # N*1*new_H*1*1
        list.append(cov)
    cov = np.squeeze(np.array(list)).transpose(
        1, 2, 0).reshape(-1, 1, new_H, len(index_list)-1)  # N*1*new_H*len(index_list)-1
    return torch.from_numpy(cov)

经过上述特征提取后，得到的新的“特征图片”的维数是$36\times3$。我们后续会将其进行池化和展平。注意到，这36行数据的上下位置不影响池化和展平操作得到的结果（展平后每个量的地位都一样），因此原始输入数据的$9\times30$的矩阵内部的上下可以任意排列。这也避免了卷积神经网络处理图片像素数据时只能感知局部数据的问题。

基于单变量的特征提取层——以`ts_stddev`为例

基于单变量进行特征提取的步骤为：

取出一行数据。
对于取出的一行数据，给定步长stride，在时间维度上对这一行数据进行遍历，计算这一行数据的标准差。例如，当$stride=3$时，下一次计算将在时间维度上往右步进3步，我们将进行$\frac{30}{3}=10$次运算。
将运算结果整理到新的矩阵，得到新的“特征图片”，作为后续池化层的输入。

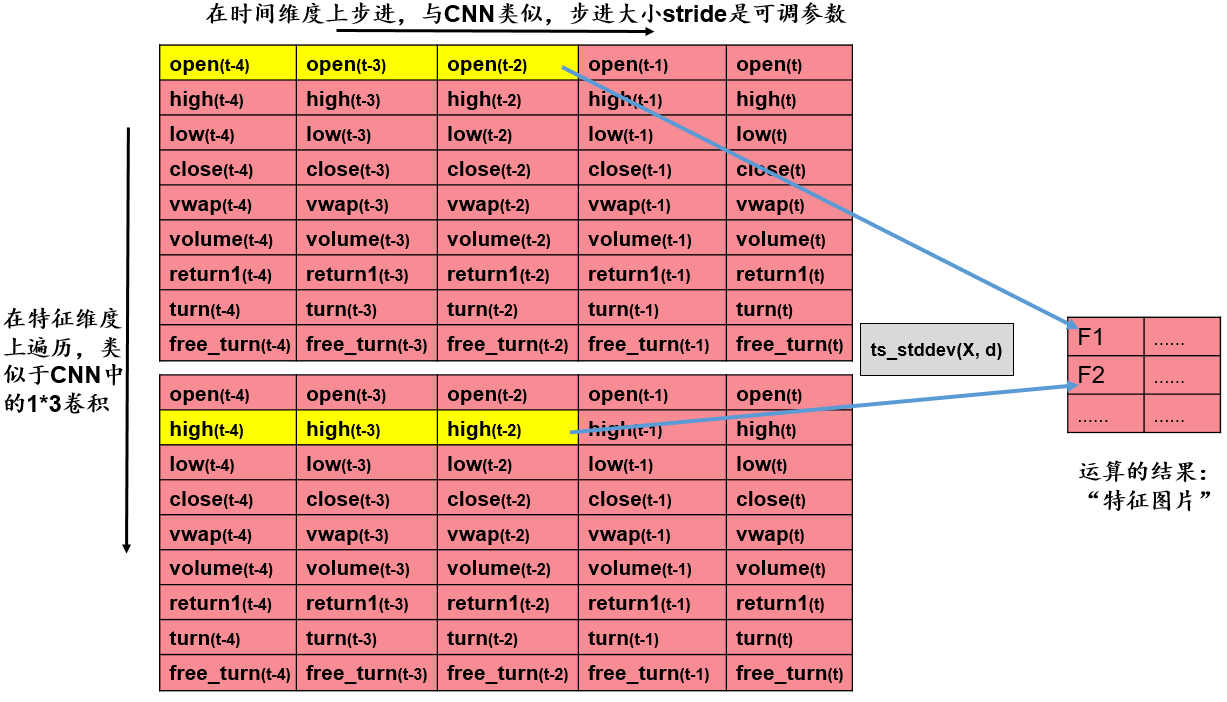
从9行数据中任取1行，有$\tbinom{9}{1}=9$种取法。假设我们设定步长为10，则得到的新的“特征图片”的维数是9*3。

基于单变量的特征提取层——代码实现

单变量的特征提取只需给定原始数据Matrix和每次遍历运算的起始索引列表index_list。

# 过去 d 天 X 值构成的时序数列的标准差
def ts_stddev4d(self, Matrix):
    # 只需要对单变量做卷积操作, 不需要将变量两两组合。因此输出的 H 可以保持和输入的 H 一致
    new_H = Matrix.shape[2]
    index_list = self.index_list
    list = []  # 存放长度为len(index_list)-1的标准差
    for i in range(len(index_list)-1):
        start_index = index_list[i]
        end_index = index_list[i+1]
        data = Matrix[:, :, :, start_index:end_index]  # N*1*H*d
        std = data.std(axis=3, keepdims=True)  # N*1*H*1
        list.append(std)
    std4d = np.squeeze(np.array(list)).transpose(
        1, 2, 0).reshape(-1, 1, new_H, len(index_list)-1)  # N*1*new_H*len(index_list)-1
    return torch.from_numpy(std4d)

# 过去 d 天 X 值构成的时序数列的平均值除以标准差
def ts_zcore4d(self, Matrix):
    # 只需要对单变量做卷积操作, 不需要将变量两两组合。因此输出的 H 可以保持和输入的 H 一致
    new_H = Matrix.shape[2]
    index_list = self.index_list
    list = []  # 存放长度为len(index_list)-1的zcore
    for i in range(len(index_list)-1):
        start_index = index_list[i]
        end_index = index_list[i+1]
        data = Matrix[:, :, :, start_index:end_index]  # N*1*H*d
        mean = data.mean(axis=3, keepdims=True)  # N*1*H*1
        std = data.std(axis=3, keepdims=True) + \
            0.01  # N*1*H*1, 加上0.01, 防止除以0
        list.append(mean/std)
    zscore = np.squeeze(np.array(list)).transpose(
        1, 2, 0).reshape(-1, 1, new_H, len(index_list)-1)  # N*1*new_H*len(index_list)-1
    return torch.from_numpy(zscore)

# (X - delay(X, d))/delay(X, d)-1, 其中 delay(X, d)为 X 在 d 天前的取值
def ts_return4d(self, Matrix):
    # 只需要对单变量做卷积操作, 不需要将变量两两组合。因此输出的 H 可以保持和输入的 H 一致
    new_H = Matrix.shape[2]
    index_list = self.index_list
    list = []  # 存放长度为len(index_list)-1的return
    for i in range(len(index_list)-1):
        start_index = index_list[i]
        end_index = index_list[i+1]
        data = Matrix[:, :, :, start_index:end_index]  # N*1*H*d
        # N*1*H*1, 在分母加上0.01, 防止除以0
        return_ = data[:, :, :, -1]/(data[:, :, :, 0]+0.01)-1
        list.append(return_)
    ts_return = np.squeeze(np.array(list)).transpose(
        1, 2, 0).reshape(-1, 1, new_H, len(index_list)-1)  # N*1*new_H*len(index_list)-1
    return torch.from_numpy(ts_return)

# 过去 d 天 X 值构成的时序数列的加权平均值, 权数为 d, d – 1, …, 1(权数之和应为 1, 需进行归一化处理), 其中离现在越近的日子权数越大
def ts_decaylinear4d(self, Matrix):
    new_H = Matrix.shape[2]
    index_list = self.index_list
    list = []  # 存放长度为len(index_list)-1的加权平均值
    for i in range(len(index_list)-1):
        start_index = index_list[i]
        end_index = index_list[i+1]
        range_ = end_index-start_index
        weight = np.arange(1, range_+1)
        weight = weight/weight.sum()  # 权重向量
        data = Matrix[:, :, :, start_index:end_index]  # N*1*H*d
        wd = (data*weight).sum(axis=3, keepdims=True)  # N*1*H*1
        list.append(wd)
    ts_decaylinear = np.squeeze(np.array(list)).transpose(
        1, 2, 0).reshape(-1, 1, new_H, len(index_list)-1)  # N*1*new_H*len(index_list)-1
    return torch.from_numpy(ts_decaylinear)

# 过去 d 天 X 值构成的时序数列的平均值
def ts_mean4d(self, Matrix):
    new_H = Matrix.shape[2]
    index_list = self.index_list
    list = []  # 存放长度为len(index_list)-1的平均值
    for i in range(len(index_list)-1):
        start_index = index_list[i]
        end_index = index_list[i+1]
        data = Matrix[:, :, :, start_index:end_index]  # N*1*H*d
        mean_ = data.mean(axis=3, keepdims=True)  # N*1*H*1
        list.append(mean_)
    ts_mean = np.squeeze(np.array(list)).transpose(
        1, 2, 0).reshape(-1, 1, new_H, len(index_list)-1)  # N*1*new_H*len(index_list)-1
    return torch.from_numpy(ts_mean)

上述7个函数就相当于定义好了卷积操作的“卷积核”，并且这些操作中没有需要优化的参数，只需要按照给定的运算符进行前向传播。

图像识别领域中的卷积操作是需要优化卷积核的，这也是和图像识别领域中的卷积操作有区别的地方。

批标准化层（Batch Normalization）

Batch Normalization通过将每一层的原始输出进行标准化（减去均值，除以标准差），还可以乘以$\gamma$（Scale），再加上$\beta$（Offset）。$\gamma$和$\beta$都是超参数，可以用神经网络训练它们。

具体的数学公式如下。

求第$l$层的批均值： $\mu=\frac{1}{m} \sum_{i=1}^m Z^{l(i)}$ 求第$l$层的批方差： $\sigma^2=\frac{1}{m} \sum_{i=1}^m\left(Z^{l(i)}-\mu\right)^2$ 批标准化的结果： $\hat{Z}^l=\gamma * \frac{Z^l-\mu}{\sqrt{\sigma^2+\varepsilon}}+\beta$ 经过上述操作，即可将$Z^l$转换为$\hat{Z}^l$。

在批标准化中，可优化的参数是$\gamma$和$\beta$。如果没有$\gamma$和$\beta$，则批标准化的运算就为常规的 z-score 标准化。

关于Batch Normalization的笔记可以参考https://fengchao.pro/post/batch-normalization/

池化层

在AlphaNet-V1中，池化层与传统的图像识别中的池化层一致，都是对某个区域的数据提取最大值、平均值和最小值。

由于PyTorch中没有内置最小池化层，我们可以将数据取相反数后，进行最大池化，再将最大池化的结果取相反数，就可以实现最小池化。

# 池化层, 尺度为1*d
self.max_pool = nn.MaxPool2d(kernel_size=(1, self.d))
self.avg_pool = nn.AvgPool2d(kernel_size=(1, self.d))
# 最小池化等价于相反数的最大池化, 后续会对结果取反
self.min_pool = nn.MaxPool2d(kernel_size=(1, self.d))

特征提取层和池化层的特征维数变化分析

在经过特征提取层、池化层后（批标准化层不改变特征维数，因此不考虑），将特征提取层和池化层的输出均展平后再拼接，得到$702\times1$的特征。

下面解释维数为$702\times 1$是如何得到的。

特征提取层展平后得到$351\times1$的特征。

有2个特征提取层是基于双变量的，它们的输出维数是$36\times3$。其他5个特征提取层都是基于单变量的，它们的输出维数是$9\times3$。
因此，特征提取层展平后得到$(2\times36+5\times9)\times3=117\times3=351$维特征。

池化层展平后也会得到$351\times1$的特征。

池化层的输入就是特征提取层的输出，因此池化层的输入是$117\times3$。
池化操作的步长stride是len(index_list)-1$=3$，即最大池化、平均池化和最小池化都将$117\times3$转换为$117\times1$的矩阵。
将3个$117\times1$的矩阵展平后，得到$3*117=351$维特征。

将特征提取层和池化层的输出均展平后再拼接，得到$351+351=702$维特征。

全连接层

全连接层包含30个神经元，接受输入为$702\times 1$的矩阵，经过一个隐藏层转换为$30\times1$的矩阵，经过RELU激活函数、Dropout Rate为0.5，再输出到$1*1$的神经元作为预测结果。

data = self.fc1(data) # N*30
data = self.relu(data)
data = self.dropout(data)
data = self.fc2(data) # N*1
# 线性激活函数, 无需再进行激活
data = data.to(torch.float)

继承`nn.module`类，改写前向传播`forward`函数

为了让我们自定义的函数在神经网络中能够运行，我们需要继承nn.module类并改写前向传播forward函数。

自定义特征提取层、池化层的代码实现

自定义的Inception类实现了特征提取层（以及随后的批标准化）、池化层（以及随后的批标准化），并将输出结果展平成$702\times 1$的矩阵。

具体的运算符函数在前面已经定义过了，这里不再详细展开。

class Inception(nn.Module):
    """
    Inception, 用于提取时间序列的特征, 具体操作包括：

    1. kernel_size和stride均为d=10的特征提取层, 类似于卷积层，用于提取时间序列的特征. 具体包括:

        1. ts_corr4d: 过去 d 天 X 值构成的时序数列和 Y 值构成的时序数列的相关系数
        2. ts_cov4d: 过去 d 天 X 值构成的时序数列和 Y 值构成的时序数列的协方差
        3. ts_stddev4d: 过去 d 天 X 值构成的时序数列的标准差
        4. ts_zscore4d: 过去 d 天 X 值构成的时序数列的平均值除以标准差
        5. ts_return4d: (X - delay(X, d))/delay(X, d)-1, 其中delay(X, d)为 X 在 d 天前的取值
        6. ts_decaylinear4d: 过去 d 天 X 值构成的时序数列的加权平均值，权数为 d, d – 1, …, 1(权数之和应为 1，需进行归一化处理)，其中离现在越近的日子权数越大
        7. ts_mean4d: 过去 d 天 X 值构成的时序数列的平均值

        各操作得到的张量维数：
        1. 由于涉及两个变量的协方差, 因此ts_corr4d和ts_cov4d的输出为 N*1*36*3
        2. 其余操作均只涉及单变量的时序计算, 因此输出为 N*1*9*3

    2. 对第1步的输出进行Batch Normalization操作, 输出维数仍为 N*1*36*3 或 N*1*9*3

    3. 对于第2步得到的张量, kernel_size为3的池化层. 具体包括:
        1. max_pool: 过去 d 天 X 值构成的时序数列的最大值
        2. avg_pool: 过去 d 天 X 值构成的时序数列的平均值
        3. min_pool: 过去 d 天 X 值构成的时序数列的最小值

        以上三个操作的输出均为 N*1*117*1
    
    4. 对第3步的输出进行Batch Normalization操作, 输出维数仍为 N*1*117*1

    5. 将第2步和第4步的输出展平后进行拼接, 得到的张量维数为 N*(2*36*3+5*9*3+3*117) = N*702

    """

    def __init__(self, combination, combination_rev, index_list):
        """
        combination: 卷积操作时需要的两列数据的组合
        combination_rev: 卷积操作时需要的两列数据的组合, 与combination相反
        index_list: 卷积操作时需要的时间索引
        
        """

        super(Inception, self).__init__()
        # 卷积操作时需要的两列数据的组合
        self.combination = combination
        self.combination_rev = combination_rev

        # 卷积操作时需要的时间索引
        self.index_list = index_list
        self.d = len(index_list)-1

        # 卷积操作后的Batch Normalization层
        self.bc1 = nn.BatchNorm2d(1)
        self.bc2 = nn.BatchNorm2d(1)
        self.bc3 = nn.BatchNorm2d(1)
        self.bc4 = nn.BatchNorm2d(1)
        self.bc5 = nn.BatchNorm2d(1)
        self.bc6 = nn.BatchNorm2d(1)
        self.bc7 = nn.BatchNorm2d(1)

        # 池化层, 尺度为1*d
        self.max_pool = nn.MaxPool2d(kernel_size=(1, self.d))
        self.avg_pool = nn.AvgPool2d(kernel_size=(1, self.d))
        # 最小池化等价于相反数的最大池化, 后续会对结果取反
        self.min_pool = nn.MaxPool2d(kernel_size=(1, self.d))

        # 池化操作后的Batch Normalization层
        self.bc_pool1 = nn.BatchNorm2d(1)
        self.bc_pool2 = nn.BatchNorm2d(1)
        self.bc_pool3 = nn.BatchNorm2d(1)

    def forward(self, data):
        """
        data: 输入的数据, 维度为batch_size*1*9*30

        """
        # 本层的输入为batch_size*1*9*30, 在训练时不需要反向传播, 因此可以使用detach()函数
        data = data.detach().cpu().numpy()
        combination = self.combination
        combination_rev = self.combination_rev

        # 卷积操作
        conv1 = self.ts_corr4d(data, combination, combination_rev).to(torch.float)
        conv2 = self.ts_cov4d(data, combination, combination_rev).to(torch.float)
        conv3 = self.ts_stddev4d(data).to(torch.float)
        conv4 = self.ts_zcore4d(data).to(torch.float)
        conv5 = self.ts_return4d(data).to(torch.float)
        conv6 = self.ts_decaylinear4d(data).to(torch.float)
        conv7 = self.ts_mean4d(data).to(torch.float)

        # 卷积操作后的Batch Normalization
        batch1 = self.bc1(conv1)
        batch2 = self.bc2(conv2)
        batch3 = self.bc3(conv3)
        batch4 = self.bc4(conv4)
        batch5 = self.bc5(conv5)
        batch6 = self.bc6(conv6)
        batch7 = self.bc7(conv7)

        # 在 H 维度上进行特征拼接
        feature = torch.cat(
            [batch1, batch2, batch3, batch4, batch5, batch6, batch7], axis=2)  # N*1*(2*36+5*9)*3 = N*1*117*3

        # 同时将特征展平, 准备输入到全连接层
        feature_flatten = feature.flatten(start_dim=1)  # N*(117*3) = N*351

        # 对多通道特征进行池化操作, 每层池化后面都有Batch Normalization
        # 最大池化
        maxpool = self.max_pool(feature)  # N*1*117*1
        maxpool = self.bc_pool1(maxpool)
        # 平均池化
        avgpool = self.avg_pool(feature)  # N*1*117*1
        avgpool = self.bc_pool2(avgpool)
        # 最小池化
        # N*1*117*1, 最小池化等价于相反数的最大池化, 并对结果取反
        minpool = -self.min_pool(-1*feature)
        minpool = self.bc_pool3(minpool)
        # 特征拼接
        pool_cat = torch.cat([maxpool, avgpool, minpool],
                             axis=2)  # N*1*(3*117)*1 = N*1*351*1
        # 将池化层的特征展平
        pool_cat_flatten = pool_cat.flatten(start_dim=1)  # N*351

        # 拼接展平后的特征
        feature_final = torch.cat(
            [feature_flatten, pool_cat_flatten], axis=1)  # N*(351+351) = N*702
        return feature_final

    # 过去 d 天 X 值构成的时序数列和 Y 值构成的时序数列的相关系数
    def ts_corr4d(self, Matrix, combination, combination_rev):
        ...

    # 过去 d 天 X 值构成的时序数列和 Y 值构成的时序数列的协方差
    def ts_cov4d(self, Matrix, combination, combination_rev):
        ...

    # 过去 d 天 X 值构成的时序数列的标准差
    def ts_stddev4d(self, Matrix):
        ...

    # 过去 d 天 X 值构成的时序数列的平均值除以标准差
    def ts_zcore4d(self, Matrix):
        ...

    # (X - delay(X, d))/delay(X, d)-1, 其中 delay(X, d)为 X 在 d 天前的取值
    def ts_return4d(self, Matrix):
        ...

    # 过去 d 天 X 值构成的时序数列的加权平均值, 权数为 d, d – 1, …, 1(权数之和应为 1, 需进行归一化处理), 其中离现在越近的日子权数越大
    def ts_decaylinear4d(self, Matrix):
        ...

    # 过去 d 天 X 值构成的时序数列的平均值
    def ts_mean4d(self, Matrix):
        ...

自定义AlphaNet的代码实现

整合前面的各层，封装到AlphaNet中。

class AlphaNet(nn.Module):

    def __init__(self, combination, combination_rev, index_list, fc1_num, fc2_num, dropout_rate):
        super(AlphaNet, self).__init__()
        self.combination = combination
        self.combination_rev = combination_rev
        self.fc1_num = fc1_num
        self.fc2_num = fc2_num
        # 自定义的Inception模块
        self.Inception = Inception(combination, combination_rev, index_list)
        # 两个全连接层
        self.fc1 = nn.Linear(fc1_num, fc2_num) # 702 -> 30
        self.fc2 = nn.Linear(fc2_num, 1) # 30 -> 1
        # 激活函数
        self.relu = nn.ReLU()
        # dropout
        self.dropout = nn.Dropout(dropout_rate)
        # 初始化权重
        self._init_weights()

    def _init_weights(self):
        # 使用xavier的均匀分布对weights进行初始化
        nn.init.xavier_uniform_(self.fc1.weight)
        nn.init.xavier_uniform_(self.fc2.weight)
        # 使用正态分布对bias进行初始化
        nn.init.normal_(self.fc1.bias, std=1e-6)
        nn.init.normal_(self.fc2.bias, std=1e-6)

    def forward(self, data):
        data = self.Inception(data)  # N*702
        data = self.fc1(data) # N*30
        data = self.relu(data)
        data = self.dropout(data)
        data = self.fc2(data) # N*1
        # 线性激活函数, 无需再进行激活
        data = data.to(torch.float)

        return data

使用`torchsummary`包查看网络结构

from torchsummary import summary

test = AlphaNet(combination, combination_rev, index_list, fc1_num=702, fc2_num=30, dropout_rate=0.5)

summary(test, input_size=(1, 9, 30))

----------------------------------------------------------------
        Layer (type)               Output Shape         Param #
================================================================
       BatchNorm2d-1             [-1, 1, 36, 3]               2
       BatchNorm2d-2             [-1, 1, 36, 3]               2
       BatchNorm2d-3              [-1, 1, 9, 3]               2
       BatchNorm2d-4              [-1, 1, 9, 3]               2
       BatchNorm2d-5              [-1, 1, 9, 3]               2
       BatchNorm2d-6              [-1, 1, 9, 3]               2
       BatchNorm2d-7              [-1, 1, 9, 3]               2
         MaxPool2d-8            [-1, 1, 117, 1]               0
       BatchNorm2d-9            [-1, 1, 117, 1]               2
        AvgPool2d-10            [-1, 1, 117, 1]               0
      BatchNorm2d-11            [-1, 1, 117, 1]               2
        MaxPool2d-12            [-1, 1, 117, 1]               0
      BatchNorm2d-13            [-1, 1, 117, 1]               2
        Inception-14                  [-1, 702]               0
           Linear-15                   [-1, 30]          21,090
             ReLU-16                   [-1, 30]               0
          Dropout-17                   [-1, 30]               0
           Linear-18                    [-1, 1]              31
================================================================
Total params: 21,141
Trainable params: 21,141
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.01
Params size (MB): 0.08
Estimated Total Size (MB): 0.10
----------------------------------------------------------------

自定义的特征提取层不需要训练参数，只需要按照规定的运算函数完成前向传播即可。同样地，池化层也不需要训练参数。

需要训练的参数来自：批标准化的$\gamma$和$\beta$，全连接层的weight和bias。

载入数据

继承`Dataset`类，改写`getitem`

class FactorData(Dataset):

    def __init__(self, train_x, train_y):
        self.len = len(train_x)
        self.x_data = train_x
        self.y_data = train_y

    def __getitem__(self, index):
        """
        指定读取数据的方式: 根据索引index返回dataset[index]

        """
        return self.x_data[index], self.y_data[index]

    def __len__(self):
        return self.len

设定Batch Size

batch_size = 1000

将数据载入到DataLoader中

# 将数据载入到DataLoader中
train_data = FactorData(trainx, trainy)
train_loader = DataLoader(dataset=train_data,
                          batch_size=batch_size,
                          shuffle=False)  # 不打乱数据集
test_data = FactorData(testx, testy)
test_loader = DataLoader(dataset=test_data,
                         batch_size=batch_size,
                         shuffle=False)  # 不打乱数据集

训练和测试模型

将AlphaNet实例化

# 构建模型
alphanet = AlphaNet(combination=combination, combination_rev=combination_rev,
                    index_list=index_list, fc1_num=702, fc2_num=30, dropout_rate=0.5)

设定优化器

weight_list, bias_list = [], []
for name, p in alphanet.named_parameters():
    # 将所有的bias参数放入bias_list中
    if 'bias' in name:
        bias_list += [p]
    # 将所有的weight参数放入weight_list中
    else:
        weight_list += [p]

# weight decay: 对所有weight参数进行L2正则化
optimizer = optim.RMSprop([{'params': weight_list, 'weight_decay': 1e-5},
                           {'params': bias_list, 'weight_decay': 0}],
                          lr=1e-4,
                          momentum=0.9)

设定损失函数为均方误差MSE

# 损失函数为均方误差 MSE
criterion = nn.MSELoss()

训练和测试模型

由于AlphaNet-V1的网络结构较为简单，模型在5到10个Epoch的训练后即收敛，因此我们设定训练轮次epoch_num为5。

训练和测试模型的代码如下：

epoch_num = 5
train_loss_list = []
test_loss_list = []
best_test_epoch, best_test_loss = 0, np.inf
seed = 0
for epoch in range(1, epoch_num+1):
    train_loss, test_loss = 0, 0
    # 在训练集中训练模型
    alphanet.train()  # 关于.train()的作用，可以参考https://stackoverflow.com/questions/51433378/what-does-model-train-do-in-pytorch
    train_batch_num = 0
    for data, label in tqdm(train_loader, f'Epoch {epoch}-train', leave=False):
        train_batch_num += 1
        # 准备数据
        data, label = data.to(torch.float), label.to(torch.float)
        # 得到训练集的预测值
        out_put = alphanet(data)
        # 计算损失
        loss = criterion(out_put, label)
        # 将损失值加入到本轮训练的损失中
        train_loss += loss.item()
        # 梯度清零
        optimizer.zero_grad() # 关于.zero_grad()的作用，可以参考https://stackoverflow.com/questions/48001598/why-do-we-need-to-call-zero-grad-in-pytorch
        # 反向传播求解梯度
        loss.backward()
        # 更新权重参数
        optimizer.step()

    # 测试模式
    alphanet.eval()
    test_batch_num = 0
    with torch.no_grad():
        for data, label in tqdm(test_loader, f'Epoch {epoch}-test ', leave=False):
            test_batch_num += 1
            data, label = data.to(torch.float), label.to(torch.float)
            # 得到测试集的预测值
            y_pred = alphanet(data)
            # 计算损失
            loss = criterion(y_pred, label)
            # 将损失值加入到本轮测试的损失中
            test_loss += loss.item()

    train_loss_list.append(train_loss/train_batch_num)
    test_loss_list.append(test_loss/test_batch_num)

绘制训练集和测试集上损失的变化

# 画出损失函数的变化
fig = plt.figure(figsize=(9, 6))
# 字号
plt.rcParams['font.size'] = 16
ax = fig.add_subplot(111)
ax.plot(range(1, epoch_num+1), train_loss_list, 'r', label='train loss')
ax.plot(range(1, epoch_num+1), test_loss_list, 'b', label='test loss')
# 设置x轴刻度为整数
ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
# 设置y轴范围
ax.set_ylim(bottom=0, top=0.1)
ax.legend()
ax.set_xlabel('Epoch')
ax.set_ylabel('MSE Loss')
plt.show()

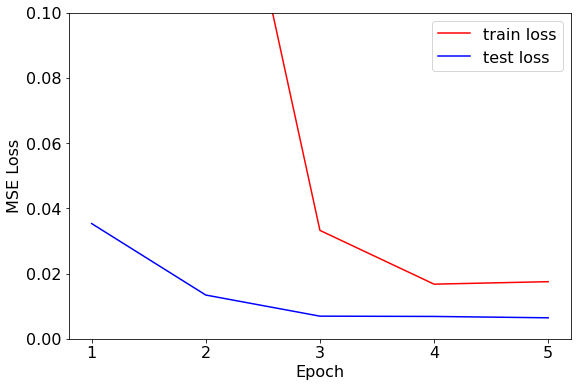
经过测试发现，训练集和验证集在训练5轮左右就已经收敛，损失已不再下降。为了探究模型给出了什么样的预测值，我们接下来比较部分样本标签的预测值和真实值。

预测值和真实值的比较

为方便查看，我们截取最后一批训练样本的前200个样本，对比模型的预测标签值和真实标签值。

# 绘制部分预测值和真实值
y_pred = y_pred.detach().numpy()
label = label.detach().numpy()

# 截取部分数据
part = range(0, 200)
plt.plot(y_pred[part], label='pred')
plt.plot(label[part], label='true')
plt.legend()
plt.show()

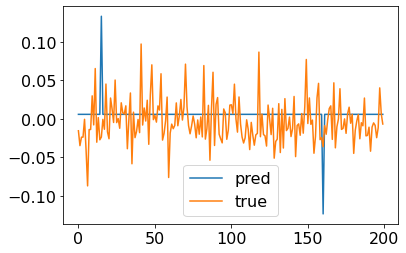
AlphaNet-V1给出的标签预测值几乎都为常数，只在少部分样本点有突出值，这并不是一个理想的收益率预测值。对于标签预测值几乎都为常数的情况，我推测原因可能是：

AlphaNet-V1的网络结构较简单，只使用了7个平行的特征提取层、3个平行的池化层和一个全连接层。简单的网络结构限制了参数的选择范围，为了减少损失，模型可能会倾向于选择常数作为标签预测值。
AlphaNet-V1用的池化层通过取最大、平均和最小的操作，将3个在时序值转换为1个值。而这三个时序值仍然具有时序信息，但简单的池化层会丧失这一时序信息。

保存模型

将模型的结构和参数均保存到本地，方便后续使用。

# 保存模型
torch.save(alphanet, 'alphanet_v1_pool.pth')

改进方向

在实证检验后，我们发现AlphaNet-V1给出的标签预测值几乎都为常数，只在少部分样本点有突出值，这并不是一个理想的收益率预测值。因此，本文尝试对AlphaNet-V1进行两方面的改进：

调整网络结构。AlphaNet-V1的网络结构较简单，我们将在AlphaNet-V3版本中加入不同步长stride的特征提取层，并将现有的池化层转换为可以记忆时序信息的门控循环单元（GRU）。
调整标签值。AlphaNet-V1预测的标签值是个股在未来10个交易日的收益率。我们将在AlphaNet-V3版本中将预测标签转换为涨跌方向（1代表上涨，即收益率大于0；0代表不变或下跌，即收益率小于或等于0）和超额收益方向（1代表收益率大于当批的平均收益率，0代表收益率小于或等于当批的平均收益率）。

搭建AlphaNet-V3

加入多步长的特征提取层

AlphaNet-V1的特征提取层中，固定步长stride=10，我们可以设定其他的步长，拓宽因子挖掘的可能性。

下面我们加入步长stride=3的特征提取层，仍使用AlphaNet-V1中的7个运算符函数。

由于步长发生变化，因此卷积操作的索引列表也发生了变化。我们需要生成两个不同的index_list，供两个步长不同的特征提取层使用。

# 根据输入的矩阵和卷积操作的步长, 计算卷积操作的索引
def get_index_list(matrix, stride):
    """
    args:
        matrix: torch.tensor, the input matrix
        stride: int, the stride of the convolution operation
    
    return:
        index_list: list, the index of the convolution operation

    """
    W = matrix.shape[3]
    if W % stride == 0:
        index_list = list(np.arange(0, W+stride, stride))
    else:
        mod = W % stride
        index_list = list(np.arange(0, W+stride-mod, stride)) + [W]
    return index_list
# 根据输入的矩阵和卷积操作的步长, 计算卷积操作的索引
# inception1模块使用的卷积操作的步长为10
index_list_1 = get_index_list(np.zeros((1,1,9,30)), 10)
# inception2模块使用的卷积操作的步长为3
index_list_2 = get_index_list(np.zeros((1,1,9,30)), 3)

在AlphaNet-V1中，我们已经编写了Inception类，它可以接收不同的index_list作为参数，因此我们只需要传入index_list_2即可实现步长为stride=3的特征提取层。

class AlphaNet(nn.Module):

    def __init__(self, combination, combination_rev, index_list_1, index_list_2, fc_num):
        super(AlphaNet, self).__init__()
        self.combination = combination
        self.combination_rev = combination_rev
        # 自定义的Inception1模块
        self.Inception_1 = Inception(combination, combination_rev, index_list_1)
        # 自定义的Inception2模块
        self.Inception_2 = Inception(combination, combination_rev, index_list_2)
        # 输出层
        self.fc = nn.Linear(fc_num, 1) # 30 -> 1
        # 初始化权重
        self._init_weights()

上面的代码完成了两个平行的特征提取层。

将池化层替换为门控循环单元（GRU）

AlphaNet-V1中的池化层仅是将特征提取层的输出在时序上取最大、平均和最小池化。若特征提取层中的步长stride=10，则池化的作用是将时序上的3个值取最大、平均和最小值，转换为1个值。这样的操作丧失了特征提取层得到的3个值本身的时序信息。

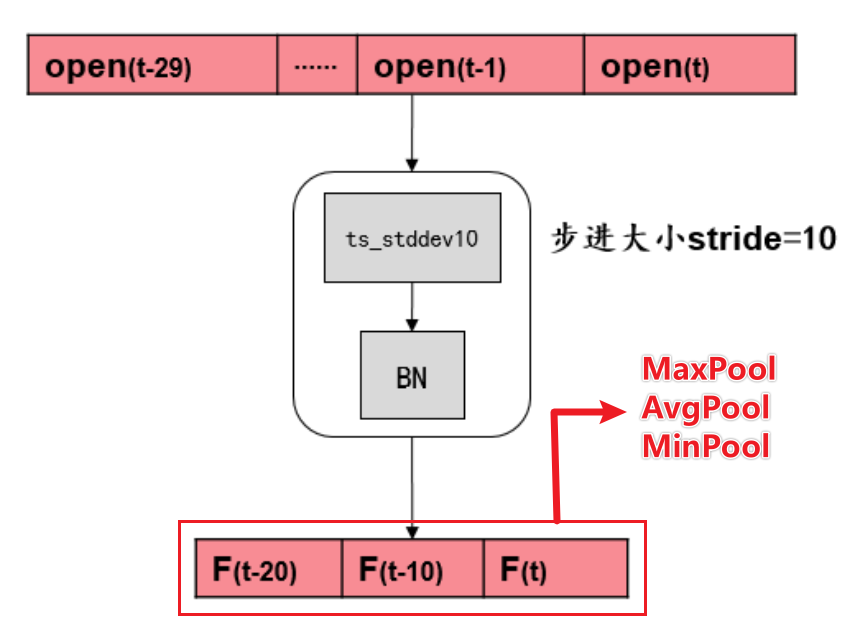
为了保留特征提取层得到的输出本身的时序信息，我们将池化层转换为门控循环单元，它是循环神经网络的一种，可以接受时序输入，并输出带有时序记忆的隐藏状态。

我们自定义的GRU层的代码如下。由于特征提取层将得到维数为$117\times3$或$117\times10$的矩阵，因此我们设定input_size=117。num_layers设为2。我们需要的输出是带有时序记忆的隐藏状态。最终将得到维数为$30$的矩阵。

class GRU(nn.Module):
    def __init__(self):
        super(GRU, self).__init__()
        self.gru = nn.GRU(input_size=117, hidden_size=30,
                          num_layers=2, batch_first=True, bidirectional=False)

    def forward(self, data):
        # N*time_step*117 -> output: torch.Size([1000, time_step, 30]), hn: torch.Size([2, 1000, 30]), 对于Inception1, time_step=3, 对于Inception2, time_step=10
        output, hn = self.gru(data)
        h = hn[-1:] # 使用最后一层hidden state的输出, h: torch.Size([1, 1000, 30])
        data = h.squeeze(0) # torch.Size([1000, 30])
        return data  # torch.Size([1000, 30])

将GRU层嵌入到自定义的Inception类中：

class Inception(nn.Module):
    """
    Inception, 用于提取时间序列的特征, 具体操作包括：

    1. kernel_size和stride为d=10或3的特征提取层, 类似于卷积层，用于提取时间序列的特征. 具体包括:(下面以d=10为例)

        1. ts_corr4d: 过去 d 天 X 值构成的时序数列和 Y 值构成的时序数列的相关系数
        2. ts_cov4d: 过去 d 天 X 值构成的时序数列和 Y 值构成的时序数列的协方差
        3. ts_stddev4d: 过去 d 天 X 值构成的时序数列的标准差
        4. ts_zscore4d: 过去 d 天 X 值构成的时序数列的平均值除以标准差
        5. ts_return4d: (X - delay(X, d))/delay(X, d)-1, 其中delay(X, d)为 X 在 d 天前的取值
        6. ts_decaylinear4d: 过去 d 天 X 值构成的时序数列的加权平均值，权数为 d, d – 1, …, 1(权数之和应为 1，需进行归一化处理)，其中离现在越近的日子权数越大
        7. ts_mean4d: 过去 d 天 X 值构成的时序数列的平均值

        各操作得到的张量维数：
        1. 由于涉及两个变量的协方差, 因此ts_corr4d和ts_cov4d的输出为 N*1*36*3
        2. 其余操作均只涉及单变量的时序计算, 因此输出为 N*1*9*3

    2. 对第1步的输出进行Batch Normalization操作, 输出维数仍为 N*1*36*3 或 N*1*9*3

    3. 对第2步的输出, 在 H 维度上拼接, 输出维数为 N*1*(2*36+5*9)*3 = N*1*117*3

    4. 对第3步的输出, 使用GRU进行特征提取, 输出维数为 N*30

    """

    def __init__(self, combination, combination_rev, index_list):
        """
        combination: 卷积操作时需要的两列数据的组合
        combination_rev: 卷积操作时需要的两列数据的组合, 与combination相反
        index_list: 卷积操作时需要的时间索引
        
        """

        super(Inception, self).__init__()
        # 卷积操作时需要的两列数据的组合
        self.combination = combination
        self.combination_rev = combination_rev

        # 卷积操作时需要的时间索引
        self.index_list = index_list

        # 卷积操作后的Batch Normalization层
        self.bc1 = nn.BatchNorm2d(1)
        self.bc2 = nn.BatchNorm2d(1)
        self.bc3 = nn.BatchNorm2d(1)
        self.bc4 = nn.BatchNorm2d(1)
        self.bc5 = nn.BatchNorm2d(1)
        self.bc6 = nn.BatchNorm2d(1)
        self.bc7 = nn.BatchNorm2d(1)

        # GRU层
        self.GRU = GRU()

    def forward(self, data):
        """
        data: 输入的数据, 维度为batch_size*1*9*30

        """
        # 本层的输入为batch_size*1*9*30, 在训练时不需要反向传播, 因此可以使用detach()函数
        data = data.detach().cpu().numpy()
        combination = self.combination
        combination_rev = self.combination_rev

        # 卷积操作
        conv1 = self.ts_corr4d(data, combination, combination_rev).to(torch.float)
        conv2 = self.ts_cov4d(data, combination, combination_rev).to(torch.float)
        conv3 = self.ts_stddev4d(data).to(torch.float)
        conv4 = self.ts_zcore4d(data).to(torch.float)
        conv5 = self.ts_return4d(data).to(torch.float)
        conv6 = self.ts_decaylinear4d(data).to(torch.float)
        conv7 = self.ts_mean4d(data).to(torch.float)

        # 卷积操作后的Batch Normalization
        batch1 = self.bc1(conv1)
        batch2 = self.bc2(conv2)
        batch3 = self.bc3(conv3)
        batch4 = self.bc4(conv4)
        batch5 = self.bc5(conv5)
        batch6 = self.bc6(conv6)
        batch7 = self.bc7(conv7)

        # 在 H 维度上进行特征拼接
        feature = torch.cat(
            [batch1, batch2, batch3, batch4, batch5, batch6, batch7], axis=2)  # N*1*(2*36+5*9)*3 = N*1*117*3

        # GRU层
        feature = feature.squeeze(1)  # N*1*117*3 -> N*117*3
        feature = feature.permute(0, 2, 1)  # N*117*3 -> N*3*117
        feature = self.GRU(feature)  # N*3*117 -> N*30

        return feature

使用`torchsummary`包查看网络结构

test = AlphaNet(combination, combination_rev, index_list_1, index_list_2, fc_num=60)

summary(test, input_size=(1, 9, 30))

----------------------------------------------------------------
        Layer (type)               Output Shape         Param #
================================================================
       BatchNorm2d-1             [-1, 1, 36, 3]               2
       BatchNorm2d-2             [-1, 1, 36, 3]               2
       BatchNorm2d-3              [-1, 1, 9, 3]               2
       BatchNorm2d-4              [-1, 1, 9, 3]               2
       BatchNorm2d-5              [-1, 1, 9, 3]               2
       BatchNorm2d-6              [-1, 1, 9, 3]               2
       BatchNorm2d-7              [-1, 1, 9, 3]               2
               GRU-8  [[-1, 3, 30], [-1, 2, 30]]               0
               GRU-9                   [-1, 30]               0
        Inception-10                   [-1, 30]               0
      BatchNorm2d-11            [-1, 1, 36, 10]               2
      BatchNorm2d-12            [-1, 1, 36, 10]               2
      BatchNorm2d-13             [-1, 1, 9, 10]               2
      BatchNorm2d-14             [-1, 1, 9, 10]               2
      BatchNorm2d-15             [-1, 1, 9, 10]               2
      BatchNorm2d-16             [-1, 1, 9, 10]               2
      BatchNorm2d-17             [-1, 1, 9, 10]               2
              GRU-18  [[-1, 10, 30], [-1, 2, 30]]               0
              GRU-19                   [-1, 30]               0
        Inception-20                   [-1, 30]               0
           Linear-21                    [-1, 1]              61
================================================================
Total params: 89
Trainable params: 89
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.17
Params size (MB): 0.00
Estimated Total Size (MB): 0.17
----------------------------------------------------------------

不知道为什么，这里的GRU层并没有显示待估计的参数，实际上GRU层也是需要估计非常多的参数的。

在2个特征提取层及GRU层后，将输出展平后拼接，得到$60\times1$的矩阵，直接连接到预测目标即可输出预测值，这样就构建了AlphaNet-V3。

使用`TensorBoard`查看网络结构

我们可以使用TensorBoard对模型进行可视化，主要代码如下。

from tensorboardX import SummaryWriter  # 用于进行可视化

from torchviz import make_dot

sample_data = torch.rand(1000, 1, 9, 30)
# 1. 来用tensorflow进行可视化
with SummaryWriter("./log", comment="sample_model_visualization") as sw:
    sw.add_graph(alphanet, sample_data)

# 2. 保存成pt文件后进行可视化
torch.save(alphanet, "./log/alphanet_v3_gru.pt")

# 3. 使用graphviz进行可视化
out = alphanet(sample_data)
g = make_dot(out)
g.render('alphanet_v3_gru', view=False)  # 这种方式会生成一个pdf文件

在TensorBoard中，查看网络结构如下。由于特征提取层的运算符函数太多，且有两个步长不同的的平行的特征提取层，若全部展开则宽度太大，因此这里只展开其中一个。

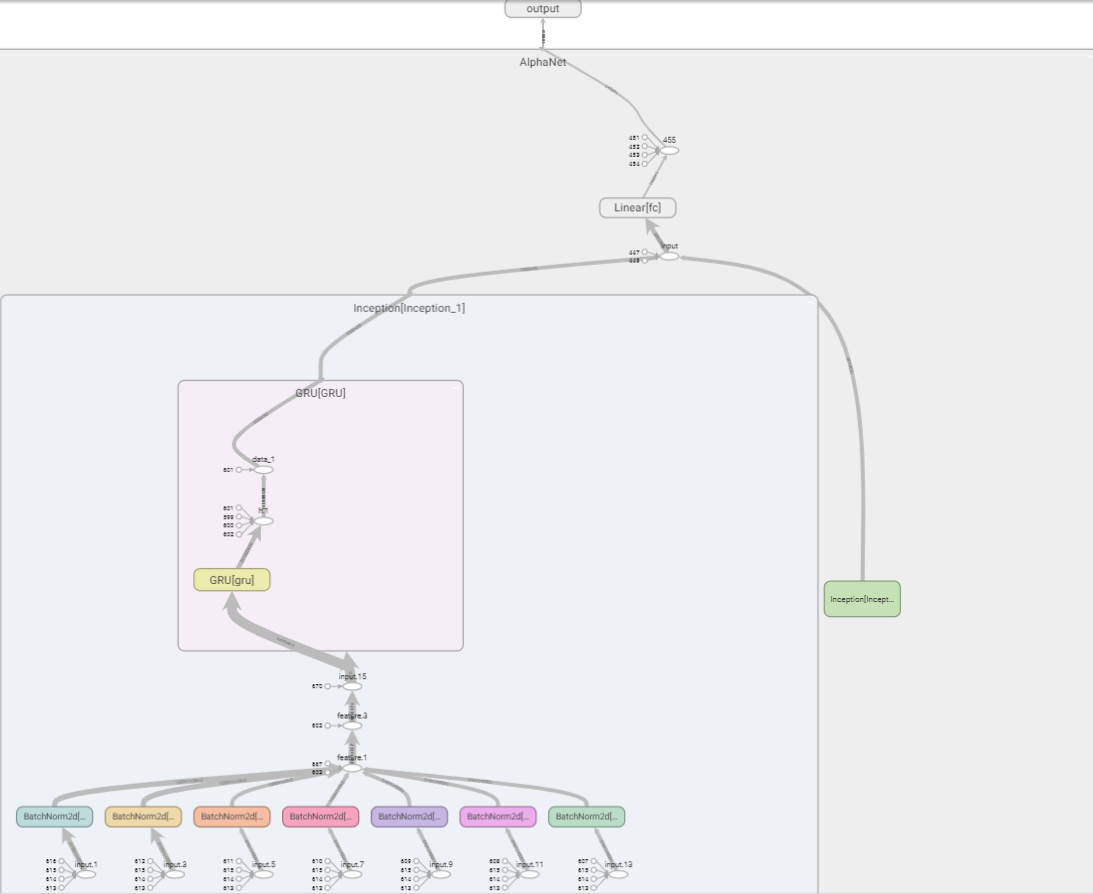
TensorBoard模型结构

训练和测试模型

相比AlphaNet-V1，AlphaNet-V3加入了步长stride=3的特征提取层、将池化层转换为保留时序信息的GRU层，模型变得更复杂。在训练模型时，训练20轮以上才显现出收敛的趋势。因此我们将epoch_num设为30。

epoch_num = 30
train_loss_list = []
test_loss_list = []
best_test_epoch, best_test_loss = 0, np.inf
for epoch in range(1, epoch_num+1):
    train_loss, test_loss = 0, 0
    # 在训练集中训练模型
    alphanet.train()  # 关于.train()的作用，可以参考https://stackoverflow.com/questions/51433378/what-does-model-train-do-in-pytorch
    train_batch_num = 0
    for data, label in tqdm(train_loader, f'Epoch {epoch}-train', leave=False):
        train_batch_num += 1
        # 准备数据
        data, label = data.to(torch.float), label.to(torch.float)
        # 得到训练集的预测值
        out_put = alphanet(data)
        # 计算损失
        loss = criterion(out_put, label)
        # 将损失值加入到本轮训练的损失中
        train_loss += loss.item()
        # 梯度清零
        optimizer.zero_grad() # 关于.zero_grad()的作用，可以参考https://stackoverflow.com/questions/48001598/why-do-we-need-to-call-zero-grad-in-pytorch
        # 反向传播求解梯度
        loss.backward()
        # 更新权重参数
        optimizer.step()

    # 测试模式
    alphanet.eval()
    test_batch_num = 0
    with torch.no_grad():
        for data, label in tqdm(test_loader, f'Epoch {epoch}-test ', leave=False):
            test_batch_num += 1
            data, label = data.to(torch.float), label.to(torch.float)
            # 得到测试集的预测值
            y_pred = alphanet(data)
            # 计算损失
            loss = criterion(y_pred, label)
            # 将损失值加入到本轮测试的损失中
            test_loss += loss.item()

    train_loss_list.append(train_loss/train_batch_num)
    test_loss_list.append(test_loss/test_batch_num)

绘制训练集和测试集上损失的变化

# 画出损失函数的变化
fig = plt.figure(figsize=(9, 6))
# 字号
plt.rcParams['font.size'] = 16
ax = fig.add_subplot(111)
ax.plot(train_loss_list, 'r', label='train loss')
ax.plot(test_loss_list, 'b', label='test loss')
# 设置y轴范围
ax.set_ylim(bottom=0, top=0.1)
ax.legend()
ax.set(xlabel='Epoch')
ax.set(ylabel='MSE Loss')
plt.show()

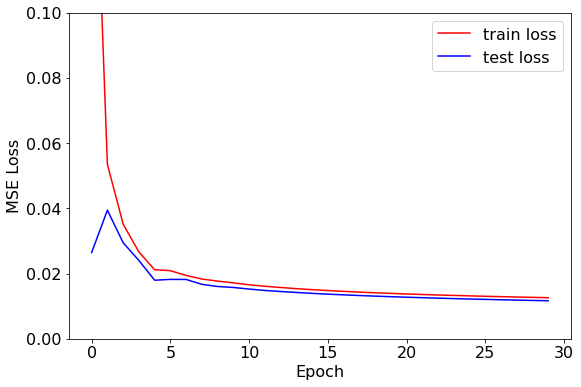
经过测试发现，训练集和验证集在训练20轮左右就已经收敛，损失已不再下降。为了探究模型给出了什么样的预测值，我们接下来比较部分样本标签的预测值和真实值。

预测值和真实值的比较

为方便查看，我们截取最后一批训练样本的前200个样本，对比模型的预测标签值和真实标签值。

# 绘制部分预测值和真实值
y_pred = y_pred.detach().numpy()
label = label.detach().numpy()
# 截取部分数据
part = range(0, 200)
plt.plot(y_pred[part], label='pred')
plt.plot(label[part], label='true')
plt.legend()
plt.show()

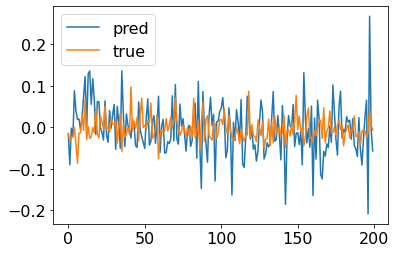
AlphaNet-V3的模型结构更复杂，输出的预测值并不全是常数，可以作为对收益率的预测值。

但我们也可以注意到AlphaNet-V3给出的收益率预测值的波动明显比真实值的波动更大，从这一点上看，预测效果并不是很理想。这可能是因为预测收益率的具体数值的难度较大，我们后续考虑将预测目标转换为收益率的方向（即个股在未来10个交易日的价格涨跌），以及超额收益的方向（即个股在未来10个交易日的收益率相对截面平均收益率的大小）。

调整预测目标：收益率的方向

为了调整预测目标，将回归问题转换为二分类问题，我们需要在代码中作如下的调整。

将预测标签转换为0和1

# 由于是分类问题, 因此将y大于0的标签设置为1，小于0的标签设置为0
trainy[trainy > 0] = 1
trainy[trainy < 0] = 0
testy[testy > 0] = 1
testy[testy < 0] = 0

全连接层最后的激活函数设为`sigmoid`，使得最终输出在0到1之间

def forward(self, data):
    data_1 = self.Inception_1(data) # N*30
    data_2 = self.Inception_2(data) # N*30
    pool_cat = torch.cat([data_1, data_2], axis=1) # N*60
    # 输出层
    data = self.fc(pool_cat)
    # 激活函数, 使输出值在0到1之间
    data = torch.sigmoid(data)
    data = data.to(torch.float)

    return data

损失函数设为`Binary Cross Entropy`

在回归问题中，我们使用的损失函数为均方误差MSE。在二分类问题中，适合使用BCELoss()，即Binary Cross Entropy Loss二元交叉熵。

# 由于是分类问题, 因此使用Binary Cross Entropy损失函数
criterion = nn.BCELoss()

绘制训练集和测试集上损失的变化

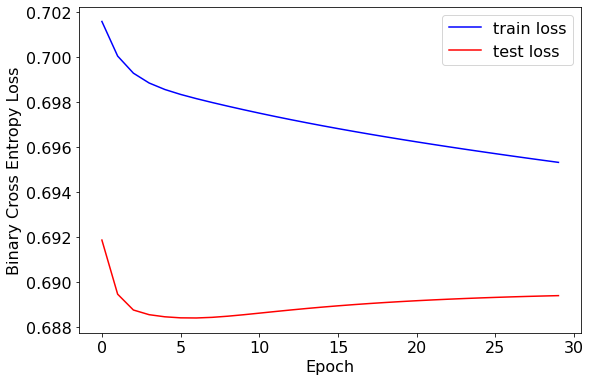
训练集和测试集的损失值较为接近，均在0.69左右。训练轮次在5轮左右时效果较好。

预测值和真实值的比较

ROC曲线

对于二分类问题，我们可以绘制ROC曲线来评价预测效果。

# 绘制ROC曲线
fpr, tpr, thresholds = metrics.roc_curve(label, y_pred)
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend(loc="lower right")
plt.show()

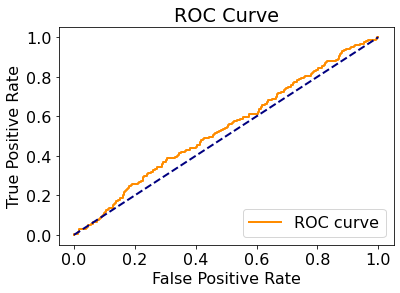
可以看到，ROC曲线仅略高于次对角线，说明预测效果仅略高于基于样本正负比率的随机猜测。

混淆矩阵

我们可以绘制混淆矩阵，查看正负例样本的预测情况。

# 绘制混淆矩阵
y_pred = np.where(y_pred > 0.5, 1, 0)
cm = metrics.confusion_matrix(label, y_pred)

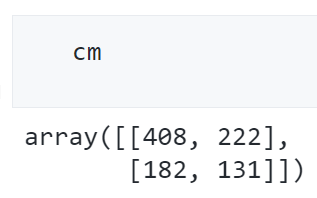
import seaborn as sn
plt.figure(figsize = (10,8))
sn.heatmap(cm, annot=True, cmap='Blues', fmt='d')
plt.xlabel('y_pred')
plt.ylabel('y_true')

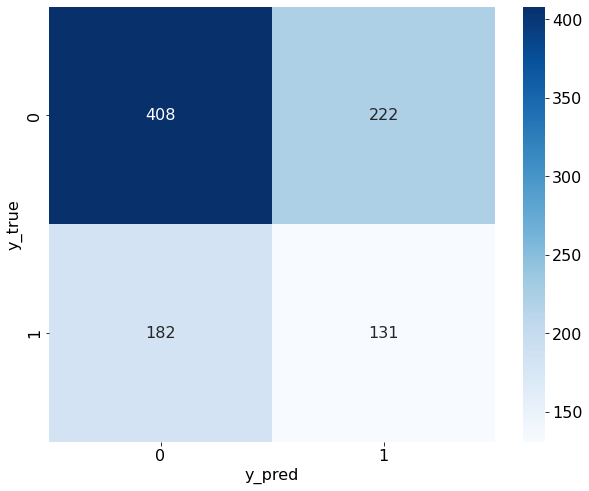
从混淆矩阵中可以看出，预测结果确实和真实数据中的正负比例很接近，说明我们的预测结果确实近似于基于样本数据的“随机猜测”。

这在信噪比极低的金融领域是可以理解的，我们的模型只用到了简单的量价数据，在生成涨跌信号的准确度上并不应奢求能获得非常好的预测效果。

调整预测目标：超额收益率的方向

由于市场存在不可分散的系统性风险，个股的收益率数值通常受市场环境的影响很大。在积极组合管理领域，投资者更希望找到能够打败市场、具有超额收益的个股。因此我们再次调整预测目标为个股在10个交易日后的超额收益的正负值。

将预测标签转换为超额收益率的正负

需要先计算截面的收益率均值，再根据个股收益率相对于截面收益率的大小，确定超额收益率的正负，并以此作为预测目标。

由于我们的样本并没有包含全市场的所有个股，因此这样的计算会有偏差。

# 由于是超额收益的分类问题, 因此将y大于trainy.mean()的标签设置为1，小于trainy.mean()的标签设置为0
train_mean_y = trainy.mean().item()
trainy[trainy > train_mean_y] = 1
trainy[trainy < train_mean_y] = 0
test_mean_y = testy.mean().item()
testy[testy > test_mean_y] = 1
testy[testy < test_mean_y] = 0

其他代码基本与“预测收益率的方向”一致，在此不再赘述。

绘制训练集和测试集上损失的变化

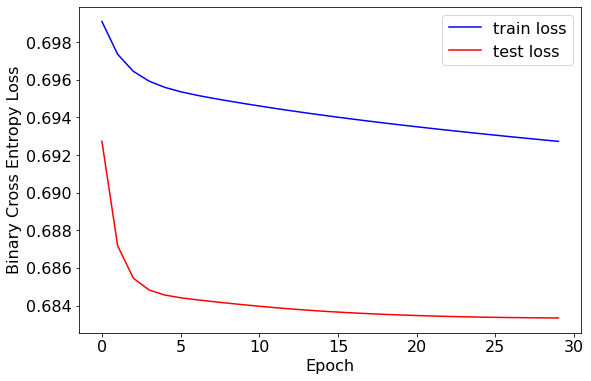
损失值得结果与“预测收益率的方向”相比略有下降，或许说明模型在预测超额收益率的方向上表现更好。

预测值和真实值的比较

ROC曲线

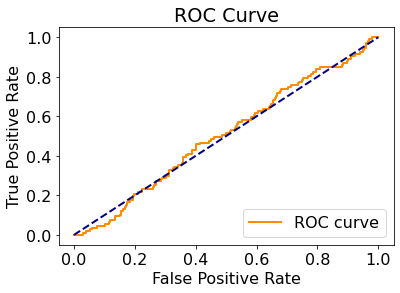
混淆矩阵

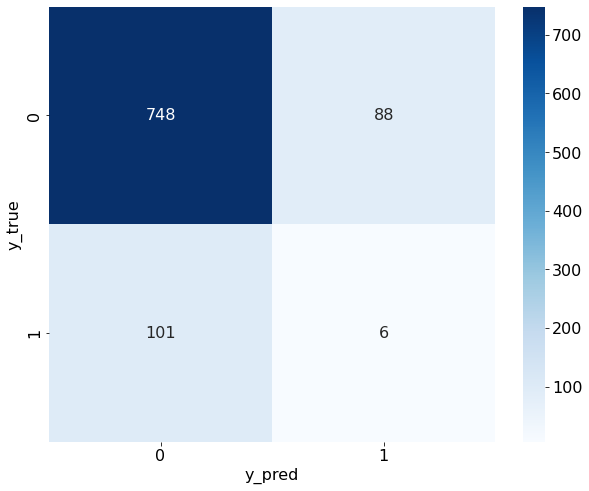
尽管我们做了多种尝试，但发现ROC曲线和混淆矩阵的表现依旧一般，模型在分类准确率上效果并不理想。

将随机森林模型作为baseline进行比较

我们的特征均为量价数据，个股在每一天有$9\times30=270$个特征。随机森林模型在训练时并不会用到全部特征，而是会随机抽取样本和特征。作为基准模型，我们不进行额外的特征工程，也不刻意调整模型参数，仅将基准结果与前面构造的AlphaNet-V3进行比较。

我们以“超额收益率的方向”作为预测目标，前文已经介绍过了AlphaNet-V3的预测效果，这里我们介绍随机森林模型进行分类预测的过程。

在前面的神经网络中，我们的输入数据是$9\times30$的矩阵，在随机森林模型中，我们需要将二维矩阵展平，再输入到模型中。

# 读取数据
X_train = np.load('../data/X_train.npy')
# # 将数据转换为二维
X_train = X_train.reshape(X_train.shape[0], -1)
y_train = np.load('../data/y_train.npy')
X_test = np.load('../data/X_test.npy')
# 将数据转换为二维
X_test = X_test.reshape(X_test.shape[0], -1)
y_test = np.load('../data/y_test.npy')
# 查看数据的大小
print("训练集特征维数: ", X_train.shape)
print("训练集标签维数: ", y_train.shape)
print("测试集特征维数: ", X_test.shape)
print("测试集标签维数: ", y_test.shape)

# 由于是超额收益的分类问题, 因此将y大于y_train.mean()的标签设置为1，小于y_train.mean()的标签设置为0
train_mean_y = y_train.mean()
y_train[y_train > train_mean_y] = 1
y_train[y_train < train_mean_y] = 0
test_mean_y = y_test.mean()
y_test[y_test > test_mean_y] = 1
y_test[y_test < test_mean_y] = 0

训练和测试模型

# 构建随机森林模型
clf = RandomForestClassifier(random_state=0, n_jobs=-1)
clf.fit(X_train, y_train)
# 在测试集上预测
y_pred = clf.predict(X_test)
y_pred_proba = clf.predict_proba(X_test)[:,1]

输出模型评价指标的函数

# 在测试集上给出模型分类的效果
def evaluate(true, pred):
    print('accuracy:{:.2%}'.format(metrics.accuracy_score(true, pred)))
    print('precision:{:.2%}'.format(metrics.precision_score(true, pred)))
    print('recall:{:.2%}'.format(metrics.recall_score(true, pred)))
    print('f1-score:{:.2%}'.format(metrics.f1_score(true, pred)))

evaluate(y_test, y_pred)

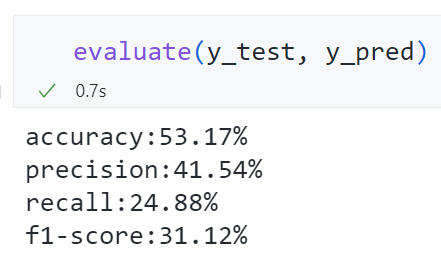
精确率、召回率均较低，基准模型的表现也不好。

特征重要性排序

随机森林模型可以基于信息增益对特征重要性进行排序。

在代码中，需要为展平后的270个特征设定名称。

# 为270个特征设定名字
feature_names = ['open', 'high', 'low', 'close', 'vwap', 'volume', 'return1', 'turn', 'free_turn']
time = range(29, -1, -1)
all_feature_names = []
for i in feature_names:
    for j in time:
        all_feature_names.append(i + '_' + str(j))
feat_importances = pd.Series(clf.feature_importances_, index=all_feature_names)

# 将特征重要性排序后绘图
ax = feat_importances.sort_values()[250:].plot(kind='barh', figsize=(12, 6))
# 设置横坐标格式
ax.xaxis.set_major_formatter(plt.FuncFormatter(lambda x, pos: "{:.2%}".format(x)))
# 设置标题
ax.set_title('Importance of Features')
# 如果不需要显示特征重要性的大小数值，可以使用下面2行代码
# for container in ax.containers:
#     ax.bar_label(container)
# 如果需要显示特征重要性的大小数值，可以使用下面的代码
x_offset = 0
y_offset = 0
for p in ax.patches:
    b = p.get_bbox()
    val = "{:.2%}".format(b.x1)
    ax.annotate(val, (b.x1 + 0.0002, b.y1 - 0.4))

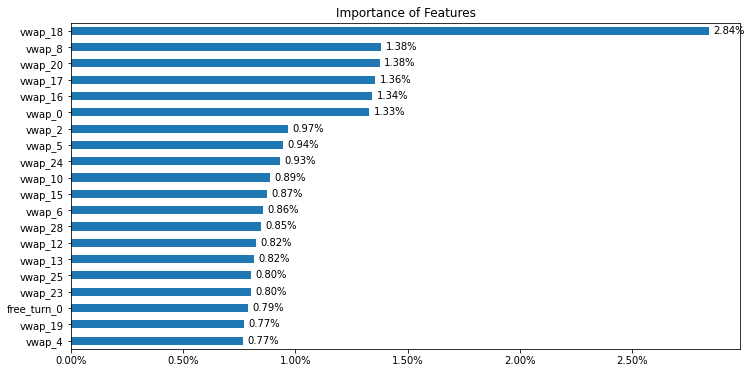
最重要的特征几乎都为vwap，说明基于成交量的加权价格可能是预测超额收益的重要因素。

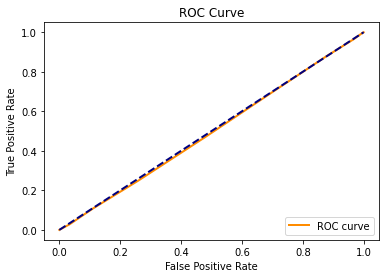
ROC曲线

# 绘制ROC曲线
fpr, tpr, thresholds = metrics.roc_curve(y_test, y_pred_proba)
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend(loc="lower right")
plt.show()

混淆矩阵

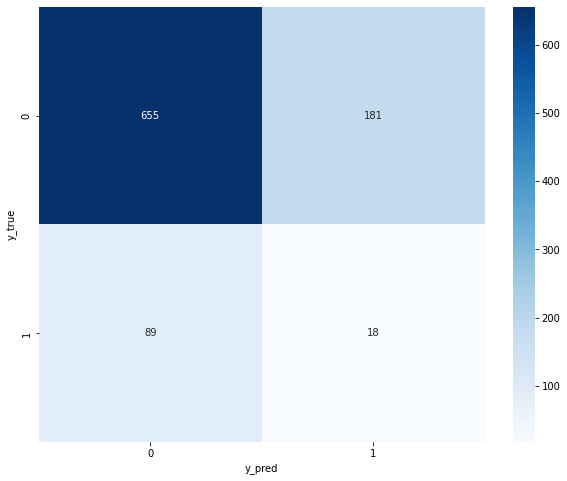
ROC曲线几乎和次对角线重合，混淆矩阵的分类准确率、召回率都不高，说明在随机森林模型上的预测效果同样不佳。

总结和结论

本文主要实现了：

基于个股在过去30个交易日的9个量价数据，构造“图片”矩阵，作为AlphaNet的输入数据。
构造自定义的特征提取层，实现2种基于双变量的特征提取层和5种基于单变量的特征提取层。
以10为步长，将自定义的特征提取层与批标准化层、最大（平均、最小）池化层、全连接层结合，以均方误差MSE为损失函数，输出收益率值的预测目标。
在训练集和验证集上做检验，发现可能是由于模型过于简单，损失值很快收敛，且预测值几乎都为常数。为此做了一些改进。
改进1：将池化层替换为门控循环单元（GRU）。改进后的预测结果能给出不同的收益率值，但波动率明显比真实值更大。
改进2：调整预测目标为收益率和方向和超额收益的方向。将全连接层的激活函数设为sigmoid，损失函数设为Binary Cross Entropy，对测试集上的预测效果进行评估，发现ROC曲线和混淆矩阵都接近随机猜测。
与基Baseline随机森林模型进行比较。我们将随机森林模型应用于对个股在未来10个交易日的超额收益的预测，发现vwap是最重要的特征。但模型评价指标也告诉我们很难准确地预测超额收益率的方向。

未来研究方向

虽然本文测试的几个模型均算不上理想，但这或许就是金融市场的特点：低信噪比、难以预测。在开始进行这个项目前，我也并不期待能搭建出预测准确率高得惊人的模型。在回顾模型是如何构建的同时，我也想到了未来可以继续拓展的方向：

扩充特征数据。本文只用到了9个量价数据，且都是日频的数据。在高频领域可以构造出更多的分钟频甚至更高频的特征数据。对于数据结构与本文相似的特征，AlphaNet都可以接受作为输入。更多的特征数据也意味着更多解释收益率的可能性，也许能提高模型的预测效果。
进一步调整模型结构和参数。由于前期搭建的模型表现并不理想，且研究时间有限，我并没有花费大量时间进行参数调优，只是参考了原始研究报告中的参数。模型中的步长、GRU层数、全连接层的设计、Dropout rate等，都可以进行参数寻优，或许能取得更好的效果。
使用更大量的数据进行训练。由于数据的可得性，本文下载15000余个样本数据耗时3个多小时。在有充足的数据来源的情况下，可以考虑对更大量的样本进行训练和测试。

参考资料

本文的研究思路来自华泰证券研究所金融工程组的两篇研究报告：《华泰人工智能系列之三十二-AlphaNet：因子挖掘神经网络》和《华泰人工智能系列之三十四-再探AlphaNet：结构和特征优化》。这两篇报告介绍了如何借鉴卷积神经网络CNN和门控循环单元GRU的思想，搭建基于量价数据进行因子挖掘的神经网络。我使用的模型参数也是基于研究报告中给出的。
本文获取数据和构造运算符函数的方法参考了知乎的回答：如何实现用遗传算法或神经网络进行因子挖掘？

AlphaNet

思路框架

问题背景

将卷积思想应用于因子挖掘

优化模型

准备数据集

训练集和测试集包含的时间段

采样的日期

采样的股票

获取单个股票在单个交易日的数据

舍弃缺失值

获取数据集

保存.npy数据到本地

搭建AlphaNet-V1

AlphaNet-V1的整体网络结构

特征提取层（类似卷积层）

基于双变量的特征提取层——以ts_corr为例

基于双变量的特征提取层——代码实现

基于单变量的特征提取层——以ts_stddev为例

基于单变量的特征提取层——代码实现

批标准化层（Batch Normalization）

池化层

特征提取层和池化层的特征维数变化分析

全连接层

继承nn.module类，改写前向传播forward函数

自定义特征提取层、池化层的代码实现

自定义AlphaNet的代码实现

使用torchsummary包查看网络结构

载入数据

继承Dataset类，改写__getitem__

设定Batch Size

将数据载入到DataLoader中

训练和测试模型

将AlphaNet实例化

设定优化器

设定损失函数为均方误差MSE

训练和测试模型

绘制训练集和测试集上损失的变化

预测值和真实值的比较

保存模型

改进方向

搭建AlphaNet-V3

加入多步长的特征提取层

将池化层替换为门控循环单元（GRU）

使用torchsummary包查看网络结构

使用TensorBoard查看网络结构

训练和测试模型

绘制训练集和测试集上损失的变化

预测值和真实值的比较

调整预测目标：收益率的方向

将预测标签转换为0和1

全连接层最后的激活函数设为sigmoid，使得最终输出在0到1之间

损失函数设为Binary Cross Entropy

绘制训练集和测试集上损失的变化

预测值和真实值的比较

ROC曲线

混淆矩阵

调整预测目标：超额收益率的方向

将预测标签转换为超额收益率的正负

绘制训练集和测试集上损失的变化

预测值和真实值的比较

ROC曲线

混淆矩阵

将随机森林模型作为baseline进行比较

训练和测试模型

输出模型评价指标的函数

特征重要性排序

ROC曲线

混淆矩阵

总结和结论

未来研究方向

参考资料

保存`.npy`数据到本地

基于双变量的特征提取层——以`ts_corr`为例

基于单变量的特征提取层——以`ts_stddev`为例

继承`nn.module`类，改写前向传播`forward`函数

使用`torchsummary`包查看网络结构

继承`Dataset`类，改写`getitem`

使用`torchsummary`包查看网络结构

使用`TensorBoard`查看网络结构

全连接层最后的激活函数设为`sigmoid`，使得最终输出在0到1之间

损失函数设为`Binary Cross Entropy`